Question

How many lines can pass through two distinct points?

Answer 1

Hint: Slope of a line passing through two distinct points $\left( {{x}_{1}},{{y}_{1}} \right)\ and\ \left( {{x}_{2}},{{y}_{2}} \right)$ will be unique and be equal to $\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$. And a line passing through a point with a given slope is unique. So, only one line can pass through two distinct points.

Complete step-by-step answer:
Let us assume two points $\left( {{x}_{1}},{{y}_{1}} \right)\ and\ \left( {{x}_{2}},{{y}_{2}} \right)$ and two lines AB and CD pass through two points $\left( {{x}_{1}},{{y}_{1}} \right)\ and\ \left( {{x}_{2}},{{y}_{2}} \right)$ is given by,
$m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$
Thus, slope of $AB=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$ and slope of $CD=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$.
Both of these lines are passing through $\left( {{x}_{1}},{{y}_{1}} \right)\ and\ \left( {{x}_{2}},{{y}_{2}} \right)$ .
We can see that, (slope of AB) = (slope of CD)
We know that two different lines passing through a given point cannot have the same slope. So, the lines AB and CD cannot be different. Thus, our assumption is wrong and AB = CD.

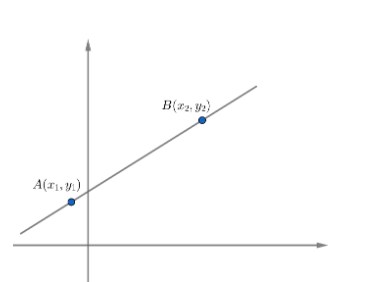
Hence, one and only one unique line can pass through two given points.

Note: In the solution, we have mentioned that two different lines passing through a fixed point cannot have the same slopes. Be careful that two different lines can have the same slope but if two different lines are passing through a fixed point, they will have different slopes.