How many lines of symmetry does a rhombus have ? (In this case we mean a rhombus that is not a square)

Question

Vedantu Content Team · Accepted Answer

Hint:- Line of symmetry to any shape is the line which divides that shape into mirror images. So, we only find a number of such lines possible in the rhombus.

Complete step-by-step answer:

Now as we know that,
Condition for any quadrilateral to be a square is the length of all the sides of that quadrilateral must be equal and all interior angles must be equal to \[90^\circ \]. And the length of the diagonals of the quadrilateral are the same.
But the condition of any quadrilateral to be a rhombus is only that the length of its all sides must be the same.
So, we can say that if the diagonals of the rhombus are also equal and it's all interior angles are equal to \[90^\circ \]. Then that rhombus will also be a square.
But here it is given that the rhombus is not a square. So, the length of the diagonals are not equal and all interior angles are not equal to \[90^\circ \].
As we know that any line will be the line of symmetry if all the images on the opposite side of that line have its mirror image same as that image if the mirror is the line itself.

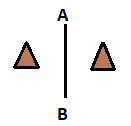
Like, in the above figure AB will be the line of symmetry because both the triangles on the opposite side of the AB are mirror images of each other and they are identical.
So, now let us draw the line of symmetry in the rhombus ABCD.

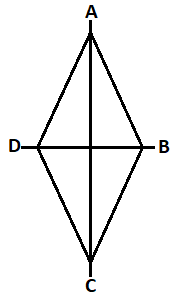
So, the AC and DB will be the line of symmetry in the rhombus ABCD because they divide the rhombus ABCD into mirror images.
Hence, the rhombus which is not a square has a total of 2 lines of symmetry.

Note:- Whenever we come up with this type of problem, we should remember that the line of symmetry in rhombus is also the diagonal of the rhombus. Because the diagonal of the rhombus divides it into two identical parts. But if the rhombus is also a square then it will have four lines of symmetry out of them 2 are the diagonals of the square and the other two are the lines which divide the opposite sides of the square into two equal halves.