Question

Locus of points from which perpendicular tangents can be drawn to the circle $$x^2+y^2=a^2$$ is
(a) A circle passing through origin
(b) A circle of radius $$2a$$
(c) Concentric circle of radius $$a\sqrt{2}$$
(d) None of these.

Answer 1

Hint: For solving this problem we assume that the point from which the tangents are drawn as $$(h,k)$$ and we take the equation of tangent as general form of equation that is $$y=mx+c$$ where $${}^{\prime }{m}^{\prime }$$ is a slope of tangent and $${}^{\prime }{c}^{\prime }$$ is some constant. By substituting the line equation we get a value of $${}^{\prime }{c}^{\prime }$$. By substituting the point in line equation we get a value of $${}^{\prime }{c}^{\prime }$$. By equating both the values of $${}^{\prime }{c}^{\prime }$$ we get the quadratic equation in $${}^{\prime }{m}^{\prime }$$ since the tangents are perpendicular by taking the product of slopes as ‘-1’ we get the required locus.

Complete step-by-step solution

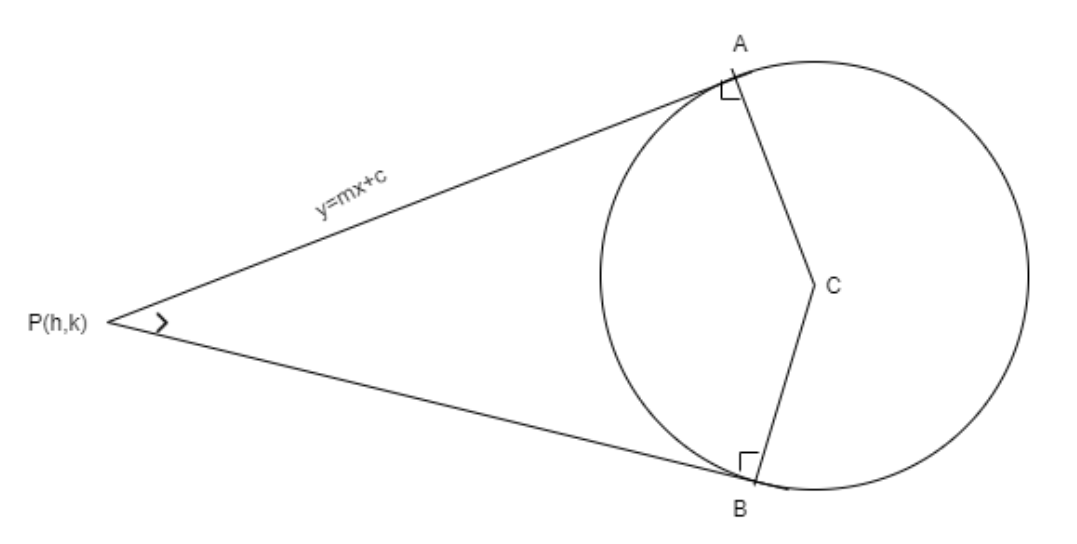
Let us assume that the point from where the tangents are drawn as $$P(h,k)$$
Let us assume that the equation of tangent as $$y=mx+c$$ where $${}^{\prime }{m}^{\prime }$$ is the slope of the tangent and $${}^{\prime }{c}^{\prime }$$ is some constant.
Here, we know that the tangent is passing through $$P(h,k)$$.
So, $$P(h,k)$$ satisfies the tangent equation. By substituting $$P(h,k)$$ in tangent equation we get
$$\begin{array}{rl}& \Rightarrow y=mx+c\\ & \Rightarrow k=mh+c\\ & \Rightarrow c=mh-k......equation(i)\end{array}$$
We know that the tangent and the circle will intersect. So, let us substitute the value of $$y=mx+c$$ in circle equation given as $$x^2+y^2=a^2$$ we get
$$\begin{array}{rl}& \Rightarrow x^2+{(mx+c)}^2=a^2\\ & \Rightarrow x^2+m^2{x}^2+2mxc+c^2=a^2\\ & \Rightarrow x^2(1+m^2)+x\left(2mc\right)+(c^2-a^2)=0\end{array}$$
Since, we know that the tangent touches the circle, the discriminant of the above equation should be zero.
The discriminant of quadratic equation $$a{x}^2+bx+c=0$$ is given as $$b^2-4ac$$.
By comparing the above equation with general equation of quadratic equation we get
$$\begin{array}{rl}& \Rightarrow {\left(2mc\right)}^2-4(c^2-a^2)(1+m^2)=0\\ & \Rightarrow 4m^2{c}^2-4c^2(1+m^2)+4a^2(1+m^2)=0\\ & \Rightarrow c^2(-1)+a^2(1+m^2)=0\\ & \Rightarrow c^2=a^2(1+m^2)....equation(ii)\end{array}$$
By substituting the value of $${}^{\prime }{c}^{\prime }$$ we got from equation (i) in equation (ii) we get
$$\begin{array}{rl}& \Rightarrow {(mh-k)}^2=a^2(1+m^2)\\ & \Rightarrow m^2{h}^2-2mhk+k^2=a^2+a^2{m}^2\\ & \Rightarrow m^2(h^2-a^2)-2mhk+(k^2-a^2)=0....equation(iii)\end{array}$$
We know that from the above equation we get two values of $${}^{\prime }{m}^{\prime }$$ which gives two equations of tangents.
We are given that the tangents are perpendicular so the product of two slopes is ‘-1’.
For the general quadratic equation $$a{x}^2+bx+c=0$$ the product of roots is given as$${\displaystyle \frac{c}{a}}$$.
By applying the product of roots to equation (iii) we get
$$\begin{array}{rl}& \Rightarrow {\displaystyle \frac{k^2-a^2}{h^2-a^2}}=-1\\ & \Rightarrow k^2-a^2=-h^2+a^2\\ & \Rightarrow h^2+k^2={\left(a\sqrt{2}\right)}^2\end{array}$$
By replacing $$(h,k)$$ by $$(x,y)$$ we get locus of point $$P(h,k)$$ as
$$\Rightarrow x^2+y^2={\left(a\sqrt{2}\right)}^2$$
Therefore, the required locus is a circle with radius $$a\sqrt{2}$$.
So, option (c) is the correct answer.

Note: This problem can be solved in other methods also.
We know that the equation of tangent to general equation of circle $$x^2+y^2=a^2$$ is given as
$$y=mx\pm a\sqrt{1+m^2}$$. We also know that point $$P(h,k)$$ lies on the tangent we can write
$$\begin{array}{rl}& \Rightarrow k=mh\pm a\sqrt{1+m^2}\\ & \Rightarrow k-mh=\pm a\sqrt{1+m^2}\end{array}$$
By squaring on both sides we get
$$\begin{array}{rl}& \Rightarrow {(mh-k)}^2=a^2(1+m^2)\\ & \Rightarrow m^2{h}^2-2mhk+k^2=a^2+a^2{m}^2\\ & \Rightarrow m^2(h^2-a^2)-2mhk+(k^2-a^2)=0....equation(iii)\end{array}$$
We know that from the above equation we get two values of $${}^{\prime }{m}^{\prime }$$ which gives two equations of tangents.
We are given that the tangents are perpendicular so the product of two slopes is ‘-1’.
For the general quadratic equation $$a{x}^2+bx+c=0$$ the product of roots is given as$${\displaystyle \frac{c}{a}}$$.
By applying the product of roots to equation (iii) we get
$$\begin{array}{rl}& \Rightarrow {\displaystyle \frac{k^2-a^2}{h^2-a^2}}=-1\\ & \Rightarrow k^2-a^2=-h^2+a^2\\ & \Rightarrow h^2+k^2={\left(a\sqrt{2}\right)}^2\end{array}$$
By replacing $$(h,k)$$ by $$(x,y)$$ we get locus of point $$P(h,k)$$ as
$$\Rightarrow x^2+y^2={\left(a\sqrt{2}\right)}^2$$
Therefore, the required locus is a circle with radius $$a\sqrt{2}$$.
So, option (c) is the correct answer.