Question

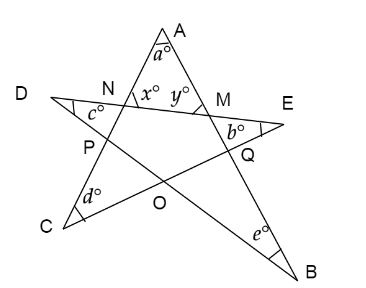
Look at the diagram of the irregular five pointed star.
(a) Explain why \[x = b + d\]
(b) Explain why \[y = c + e\]
(c) Show that the sum of the angles in the points of the star \[a + b + c + d + e\] , is \[180^\circ \]

Answer 1

Hint: In the above given question, we are given an irregular five pointed star which has different angles at each of the vertices. We have to prove the given objectives in the problem. In order to approach the solution, we have to recall two known properties in geometry. They are the angle sum property of a triangle and the exterior angle property of a triangle.

Complete step by step answer:
Given that, an irregular five pointed star AEBCD. We have to prove,
(a) \[x = b + d\]
(b) \[y = c + e\]
(c) \[a + b + c + d + e = 180^\circ \]
Now, from the figure, consider the line AMB. Since the angle of a straight line is \[180^\circ \] so we can write,
\[ \Rightarrow \angle AMD + \angle BMD = 180^\circ \]
\[ \Rightarrow y + \angle BMD = 180^\circ \] ...(1)
Also, in the triangle \[\vartriangle BMD\] , from the angle sum property of a triangle we can write,
\[ \Rightarrow c + e + \angle BMD = 180^\circ \] ...(2)
From equation (1) and (2) we have
\[ \Rightarrow y + \angle BMD = c + e + \angle BMD = 180^\circ \]
That gives us,
\[ \Rightarrow y = c + e\]
Hence, part (b) is proved.That is called the exterior angle property of a triangle.

Similarly, now consider the triangle \[\vartriangle ECN\] we have,
\[ \Rightarrow b + d + \angle ENC = 180^\circ \]
Also we have,
\[ \Rightarrow x + \angle ENC = 180^\circ \]
That gives us,
\[ \Rightarrow x + \angle ENC = b + d + \angle ENC = 180^\circ \]
\[ \Rightarrow x = b + d\]
That is the part (a) proved here.

Now, since we have proved (a) and (b) , therefore we can write
\[ \Rightarrow a + b + c + d + e\]
\[ \Rightarrow a + b + c + d + e = a + \left( {b + d} \right) + \left( {c + e} \right)\]
That gives us,
\[ \Rightarrow a + b + c + d + e = a + x + y\]
Now by the angles sum property of a triangle \[\vartriangle AMN\] , we have
\[ \Rightarrow a + b + c + d + e = 180^\circ \]
Hence, all the three objectives are proved.

Note: The angle sum property of a triangle states that the sum of all three angles of a triangle is equal to the straight angle i.e. \[180^\circ \]. Whereas , the exterior angle property of a triangle states that the sum of any two angles of a triangle is equal to the exterior angle of the third angle, when its side is extended further.