Question

Magnetic moment of an atom is the result of
1) Electron spin.
2) A change in the orbital motion of the electrons caused by an applied magnetic field.
3) Both (1) and (2).
4) None of these.

Answer 1

Hint: Magnetic moment is the strength and the orientation of a magnet. Essentially a magnetic moment originates due to the electron spinning in an orbit. It increases with increasing number of electrons which are unpaired.

Complete step by step solution:
Find the magnetic moment due to electron:
Here, we need to consider an atom, the electron moves in a circular orbit around the proton. The current would be \[I = \dfrac{Q}{T}\]. An electron that orbits around an atom is similar to the current flowing through a circular wire. We know that a current carrying wire produces a magnetic field.

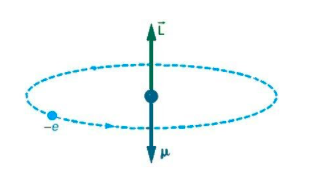
So, the magnitude of the orbital magnetic dipole moment for current loop is

$\mu = IA$ ;

Here:
I = Current;
A = Area;
And we know that \[I = \dfrac{Q}{T}\], so:

$\mu = \dfrac{e}{T}A$; ….(Q = e = charge)

Here the T is the orbital period which is given as:

$T = \dfrac{{2\pi r}}{v}$ ;

Now,

$\mu = \dfrac{e}{T}A$;
$ \Rightarrow \mu = \dfrac{e}{T}\left( {\pi {r^2}} \right)$;

Now, put the value of the time period:

$ \Rightarrow \mu = \dfrac{e}{{\dfrac{{2\pi r}}{v}}}\left( {\pi {r^2}} \right)$;
$ \Rightarrow \mu = \dfrac{{erv}}{2}$;

Now, the above equation is the magnetic moment due to an electron, we can also write it in terms of angular momentum.

$L = r \times p$;

Here:
L = Angular Momentum;
r = Distance;
p = Momentum (Linear)

Now, the angular momentum is given as$L = r \times p$, here $p = mv$ ;

$L = mvr$;

Now, write the equation $\mu = \dfrac{{erv}}{2}$in terms of r;

$\dfrac{{2\mu }}{{ev}} = r$;

Put the above relation in the formula for angular momentum $L = mvr$.

\[L = mv\left( {\dfrac{{2\mu }}{{ev}}} \right)\];
\[ \Rightarrow L = m\left( {\dfrac{{2\mu }}{e}} \right)\];

Write the equation in terms of \[\mu \]:

\[ \Rightarrow \mu = \left( {\dfrac{e}{{2m}}} \right)L\];

The above is the magnetic moment in terms of angular momentum i.e. it is the electron spin.
Form the above derivation it is clear that the Magnetic moment of an atom is the result of Electron spin which is the change in the orbital motion of the electrons caused by an applied magnetic field

Final Answer: Option “3” is correct.

Note: Here option “1” is the cause and option “2” is the reason for (cause) option “1”. Here, we need to derive the magnetic moment due to electron rotating in an orbit around the atom. We can derive Bohr’s Magneton from this equation.