
Answer
406.2k+ views
Hint: The sector is related to the circle. We explain this question by using the definition of a sector using some figures related to sectors and differentiate the major and minor sector.
The region in a circle formed by two radii and arc of the circle is called a sector.
Using this definition we explain the sector using the diagrams and define the formulas of the sector.
Complete step-by-step solution:
We are asked to explain about the major sector.
We know that the sector is related to a circle and is defined as the region formed by two radii and the arc formed by the radii.
Now, let us draw the figure that represents the above definition then we get,
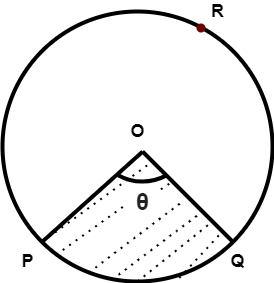
Here, we can see that the dotted region is called the sector and also the remaining part is called as sector and is given as OPQ and OPRQ respectively.
Here, we can see that the angle formed by sector OPQ at centre is $\theta <{{180}^{\circ }}$ so that the angle formed by OPRQ at centre is ${{360}^{\circ }}-\theta >{{180}^{\circ }}$
We know that the difference between major and minor is that major is having maximum part and minor is having minimum part.
Here, we can see from the figure that minor sector is OPQ and the major sector is OPRQ.
Therefore, we can conclude that the major sector is the sector having the angle formed by radii at centre is greater than ${{180}^{\circ }}$.
Now, let us give the formula of perimeter and area of the major sector.
Let us assume that the radius of the above circle is $'r'$
We know that the perimeter of an object is the sum of all lengths.
Here, we can see that the perimeter of major sector OPRQ is given as,
$\Rightarrow P=OP+arc\left( ORQ \right)+OQ$
We know that the arc length making an angle $\alpha $ at centre is given as,
$l=\dfrac{\alpha }{{{360}^{\circ }}}\times 2\pi r$
By using this formula of arc length in above equation then we get,
$\begin{align}
& \Rightarrow P=r+\left( \dfrac{{{360}^{\circ }}-\theta }{{{360}^{\circ }}}\times 2\pi r \right)+r \\
& \Rightarrow P=2r+2\pi r\left( \dfrac{{{360}^{\circ }}-\theta }{{{360}^{\circ }}} \right) \\
\end{align}$
Now, let us find the formula of area of the major sector.
We know that the area formed by two radii and arc which makes an angle $\alpha $ at centre is given as,
$A=\dfrac{\alpha }{{{360}^{\circ }}}\times \pi {{r}^{2}}$
By using this formula for the major sector OPRQ then we get,
$\begin{align}
& \Rightarrow A=\dfrac{{{360}^{\circ }}-\theta }{{{360}^{\circ }}}\times \pi {{r}^{2}} \\
& \Rightarrow A=\pi {{r}^{2}}\left( \dfrac{{{360}^{\circ }}-\theta }{{{360}^{\circ }}} \right) \\
\end{align}$
Therefore, we can conclude that the perimeter and area formulas of major sector of the above figure is given as,
$\begin{align}
& \therefore P=2r+2\pi r\left( \dfrac{{{360}^{\circ }}-\theta }{{{360}^{\circ }}} \right) \\
& \therefore A=\pi {{r}^{2}}\left( \dfrac{{{360}^{\circ }}-\theta }{{{360}^{\circ }}} \right) \\
\end{align}$
Note: The main mistake that can be done in general definition is circle is that assuming the sector and segment differently.
Sector is formed by two radii and arc induced.
Segment is formed by chord and the arc induced.
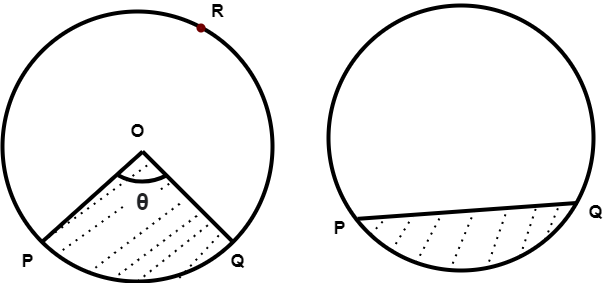
The shaded region in first figure is sector and the shaded region in second figure is segment.
There is only one case when both define the same region that is when $PQ$ is the diameter.
The region in a circle formed by two radii and arc of the circle is called a sector.
Using this definition we explain the sector using the diagrams and define the formulas of the sector.
Complete step-by-step solution:
We are asked to explain about the major sector.
We know that the sector is related to a circle and is defined as the region formed by two radii and the arc formed by the radii.
Now, let us draw the figure that represents the above definition then we get,

Here, we can see that the dotted region is called the sector and also the remaining part is called as sector and is given as OPQ and OPRQ respectively.
Here, we can see that the angle formed by sector OPQ at centre is $\theta <{{180}^{\circ }}$ so that the angle formed by OPRQ at centre is ${{360}^{\circ }}-\theta >{{180}^{\circ }}$
We know that the difference between major and minor is that major is having maximum part and minor is having minimum part.
Here, we can see from the figure that minor sector is OPQ and the major sector is OPRQ.
Therefore, we can conclude that the major sector is the sector having the angle formed by radii at centre is greater than ${{180}^{\circ }}$.
Now, let us give the formula of perimeter and area of the major sector.
Let us assume that the radius of the above circle is $'r'$
We know that the perimeter of an object is the sum of all lengths.
Here, we can see that the perimeter of major sector OPRQ is given as,
$\Rightarrow P=OP+arc\left( ORQ \right)+OQ$
We know that the arc length making an angle $\alpha $ at centre is given as,
$l=\dfrac{\alpha }{{{360}^{\circ }}}\times 2\pi r$
By using this formula of arc length in above equation then we get,
$\begin{align}
& \Rightarrow P=r+\left( \dfrac{{{360}^{\circ }}-\theta }{{{360}^{\circ }}}\times 2\pi r \right)+r \\
& \Rightarrow P=2r+2\pi r\left( \dfrac{{{360}^{\circ }}-\theta }{{{360}^{\circ }}} \right) \\
\end{align}$
Now, let us find the formula of area of the major sector.
We know that the area formed by two radii and arc which makes an angle $\alpha $ at centre is given as,
$A=\dfrac{\alpha }{{{360}^{\circ }}}\times \pi {{r}^{2}}$
By using this formula for the major sector OPRQ then we get,
$\begin{align}
& \Rightarrow A=\dfrac{{{360}^{\circ }}-\theta }{{{360}^{\circ }}}\times \pi {{r}^{2}} \\
& \Rightarrow A=\pi {{r}^{2}}\left( \dfrac{{{360}^{\circ }}-\theta }{{{360}^{\circ }}} \right) \\
\end{align}$
Therefore, we can conclude that the perimeter and area formulas of major sector of the above figure is given as,
$\begin{align}
& \therefore P=2r+2\pi r\left( \dfrac{{{360}^{\circ }}-\theta }{{{360}^{\circ }}} \right) \\
& \therefore A=\pi {{r}^{2}}\left( \dfrac{{{360}^{\circ }}-\theta }{{{360}^{\circ }}} \right) \\
\end{align}$
Note: The main mistake that can be done in general definition is circle is that assuming the sector and segment differently.
Sector is formed by two radii and arc induced.
Segment is formed by chord and the arc induced.

The shaded region in first figure is sector and the shaded region in second figure is segment.
There is only one case when both define the same region that is when $PQ$ is the diameter.



