
Make two factor trees of 32.
Answer
487.5k+ views
1 likes
Hint:
First, we will prime factorize the given number 32 to make trees with different factors. We will then select two DIFFERENT pairs of factors of 32 to mark the beginning of the tree and hence after that we will complete the remaining tree.
Complete step by step solution:
We need to find out the prime factors of 32,
To find the prime factors we need to divide the given number by the smallest prime numbers it is divisible by, hence
Prime factorization of 32 is
Where,
Where,
Where,
Hence, Using the above equations, we get
Now for our first-factor tree, we can write 32 as
The factor tree according to the above factors is
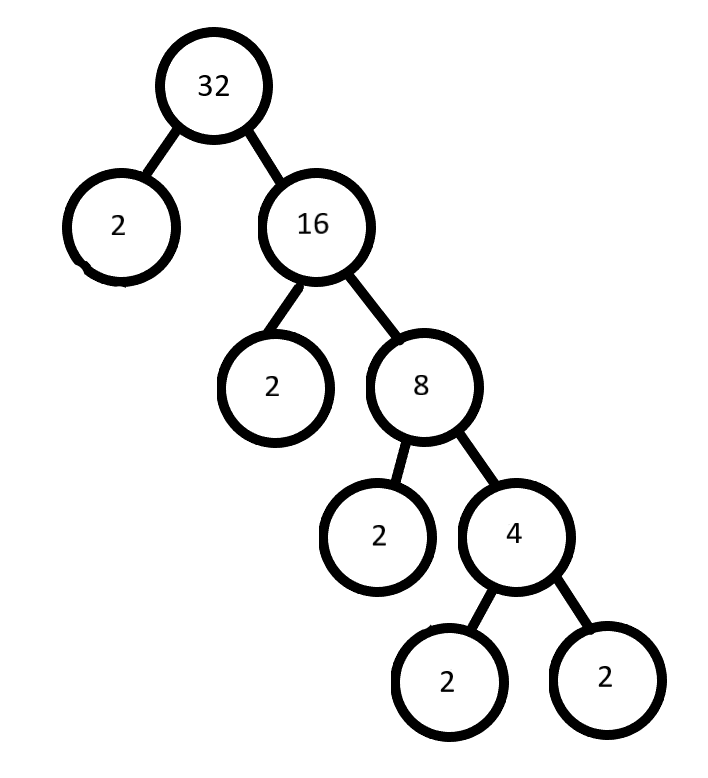
Now for our second-factor tree, we can write 32 as
So we have,
The factor tree according to the above factors is
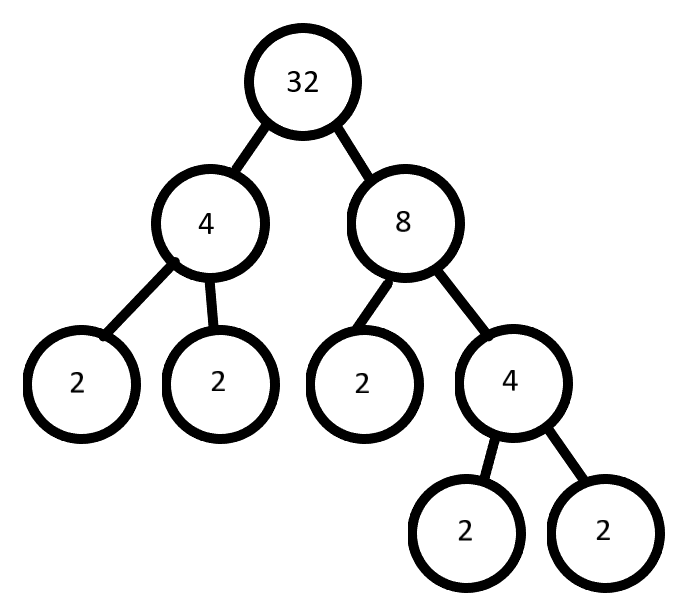
Hence, the two figures are the required factor trees.
Note:
Factor trees are the visual representation of factors of a number, though this question is very easy but prime factorization must be done by dividing the minimum prime number possible till the given number is not divisible by any number.
First, we will prime factorize the given number 32 to make trees with different factors. We will then select two DIFFERENT pairs of factors of 32 to mark the beginning of the tree and hence after that we will complete the remaining tree.
Complete step by step solution:
We need to find out the prime factors of 32,
To find the prime factors we need to divide the given number by the smallest prime numbers it is divisible by, hence
Prime factorization of 32 is
Where,
Where,
Where,
Hence, Using the above equations, we get
Now for our first-factor tree, we can write 32 as
The factor tree according to the above factors is

Now for our second-factor tree, we can write 32 as
So we have,
The factor tree according to the above factors is

Hence, the two figures are the required factor trees.
Note:
Factor trees are the visual representation of factors of a number, though this question is very easy but prime factorization must be done by dividing the minimum prime number possible till the given number is not divisible by any number.
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Out of 30 students in a class 6 like football 12 like class 7 maths CBSE

Earth rotates from West to east ATrue BFalse class 6 social science CBSE

The easternmost longitude of India is A 97circ 25E class 6 social science CBSE

Write the given sentence in the passive voice Ann cant class 6 CBSE

Convert 1 foot into meters A030 meter B03048 meter-class-6-maths-CBSE

What is the LCM of 30 and 40 class 6 maths CBSE

Trending doubts
How many millions make a billion class 6 maths CBSE

Give 10 examples for herbs , shrubs , climbers , creepers

The forces of Alexander and Porus fought on the banks class 6 social science CBSE

Four bells toll together at 900am They toll after 7811 class 6 maths CBSE

The wheel was invented at which age A Stone age B Copper class 6 social studies CBSE

The planet nearest to earth is A Mercury B Venus C class 6 social science CBSE





