Question

Marbles of diameter 1.4 cm are dropped into a beaker containing some water and are fully submerged. The diameter of the beaker is 7 cm. Find how many marbles have been dropped in it if the water rises by 5.6 cm.

Answer 1

Hint: The formula of the volume of a cylinder is given by $v=\pi {{r}^{2}}h$, where h represents the height of the cylinder and r is the radius of the cylinder. Also, the number of things or objects in the cylinder is equal to the volume of the cylinder by volume of that one object.

Complete step-by-step solution -

The marbles are always of spherical shape. So, according to the question, we have marbles of diameter 1.4 cm. The marble is represented below.

We know that diameter = 2 (radius) or radius is diameter by 2. Therefore, we have the radius of the marble as, $\dfrac{1.4}{2}=0.7cm$. Now we will find the volume of one marble. The volume of 1 marble = Volume of sphere, which is given by $\dfrac{4}{3}\pi {{r}^{3}}$, where r is the radius of the sphere. Therefore, we have, volume of 1 marble $=\dfrac{4}{3}\pi {{r}^{3}}\Rightarrow \dfrac{4}{3}\pi {{\left( 0.7 \right)}^{3}}$.
Now, we will consider the beaker. The beaker is always cylindrical in shape. The diagram of the beaker is shown below with the measurements as mentioned in the question.

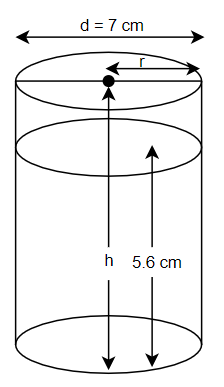
Since, the diameter is given as 7 cm, we have the radius r of the beaker as $\dfrac{7}{2}=3.5cm$. The height of the water is given as 5.6 cm. We can find the volume of the water with these values. That means we can find the space taken by the water inside the beaker. So, the volume of water $=\pi {{r}^{2}}h\Rightarrow \pi {{\left( 3.5 \right)}^{2}}\left( 5.6 \right)$.
Now, we have the volume of the water and the volume of the marble. So, by applying the formula, we can find the number of marbles dropped in it as $=\dfrac{\text{Volume of water}}{\text{Volume of 1 marble}}$. So, we get,
$\begin{align}
  & =\dfrac{\pi {{\left( 3.5 \right)}^{2}}\times \left( 5.6 \right)}{\dfrac{4}{3}\pi {{\left( 0.7 \right)}^{3}}} \\
 & =\dfrac{\pi \times 3\times {{\left( 3.5 \right)}^{2}}\times \left( 5.6 \right)}{4\pi \times {{\left( 0.7 \right)}^{3}}} \\
\end{align}$
Cancelling the similar terms and simplifying further, we get,
$=\dfrac{3\times 12.25\times 5.6}{4\times 0.343}$
Converting the decimals, we get,
$\begin{align}
  & =\dfrac{3\times 1225\times 56}{4\times 343}\times \dfrac{1000}{100\times 10} \\
 & =\dfrac{205800}{1372} \\
 & =150 \\
\end{align}$
We get the number of marbles as 150.
Hence, 150 marbles have been dropped into the beaker containing 5.6 cm raised water in it.

Note: One should remember not to get confused between the height of the beaker and the height of the water inside the beaker. These are two different heights, unless mentioned in the question. Do not forget to use units in the concluding line of the answer, if you cannot put them between the solutions. Here, $\pi $ was cancelled, but if it was not getting cancelled, we should use its value as $\pi =\dfrac{22}{7}$ instead of 3.14, since the calculations are in multiplication.