Question

Mass per unit of a semicircular disc of total mass m radius R varies linearly with radial distances from the point 0(base centre). Find the height of the centre of mass from 0.
$\begin{align}
  & \text{A}\text{. }\dfrac{2R}{\pi } \\
 & \text{B}\text{. }\dfrac{3R}{2\pi } \\
 & \text{C}\text{. }\dfrac{4R}{3\pi } \\
 & \text{D}\text{. }\dfrac{3R}{8} \\
\end{align}$

Answer 1

Hint: Centre of mass of an object is the point at which an object can be balanced and its position depends on the shape of the body as it is present at a point nearer to the more mass concentrated area.

Complete step by step answer:
Now we have to find out height of centre of mass from the point 0,

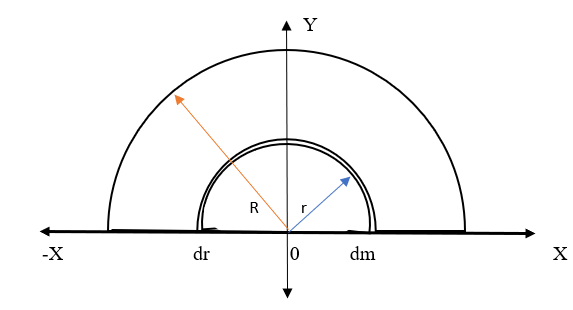
                                                 Fig. a
For this, first consider a semicircular disc of radius ‘R’ with base ‘0’ as shown in the above figure, whose mass is ‘M’ distributed uniformly over the disk.
Now, to find the centre of mass of a semicircular disc, it can be divided into several rings. Now consider one such ring of thickness ‘dr’ and radius ‘r’ and mass ‘dm’ as shown in figure a.
If we consider a circular disk, then its centre of mass lies at the centre of the disk but when we consider a semicircular disk its centre of mass shifted to above in the y-axis as shown.
So by symmetry centre of mass lie on y-axis , i.e., ${{x}_{cm}}=0$ so there exist only ${{Y}_{cm}}$
The centre of mass formula of a continuous body is given by:
${{Y}_{cm}}=\dfrac{\int{ydm}}{M}$ …….. equation (1)
Where, y is the centre of mass of the ring,
\[y=\dfrac{2r}{\pi }\] where r is the radius of the small ring.
M is the total mass of the disk
And dm is the mass of the ring
To substitute dm (mass of the small ring) in the above formula, first we have to find it.
Let us consider ring in the form of stripe as shown below:

                                           Fig. b
now we know that, to find the mass of the ring the formula is:
$dm=\dfrac{M}{A}dA$ …….. equation (2)
where, M - is the total mass of semicircular disc
A – is the area of the total semicircular disc
dA - is the area of the considered ring

Now area of small ring = length × width
 width is ‘dr’ as shown since it is a semicircle its length ‘l’ is half of the circumference of the circle,
$\therefore l=\dfrac{2\pi r}{2}=\pi r$
On substituting we get,
 $dA=\pi rdr$
on substituting above values in equation 2, we get,
$dM=\dfrac{M}{\dfrac{\pi {{r}^{2}}}{2}}dA$
$\therefore dM=\dfrac{2Mrdr}{{{R}^{2}}}$
Thus, we find the mass of the ring.
Now on substituting all the values including dm in equation (1), we get,
${{Y}_{cm}}=\dfrac{\int{\dfrac{2r2Mrdr}{\pi {{R}^{2}}}}}{M}$
Take constants out of the integral and cancelling M, we get,
${{Y}_{cm}}=\dfrac{4}{\pi {{R}^{2}}}\int_{0}^{R}{{{r}^{2}}}dr$
Limits are taken from 0 to R because we measure it from centre of the semicircle to total radius R up to edge covering the entire semicircular disc
on integrating we get,
${{Y}_{cm}}=\dfrac{4}{\pi {{R}^{2}}}\left[ \dfrac{{{r}^{3}}}{3} \right]_{0}^{R}$

substituting the limits, we get,
${{Y}_{cm}}=\dfrac{4}{\pi {{R}^{2}}}\left[ \dfrac{{{R}^{3}}}{3} \right]$
As R is in both numerator and denominator by cancelling, we get
\[\] ${{Y}_{CM}}=\dfrac{4R}{3\pi }$
Thus, the height of the centre of mass from base ‘0’ is $\dfrac{4R}{3\pi }$which means the correct option is C.

Note: Students make mistakes by confusing it with a ring and may choose option A, which is incorrect. They have asked for a disk where mass is distributed continuously. Always read questions properly.
To solve this problem you have to remember all the above formulas along with the centre of mass of the semicircular ring which is $=\dfrac{2R}{\pi }$.