
Maximum horizontal range obtained when
A).
B).
C).
D).
Answer
433.5k+ views
1 likes
Hint: Let us consider a body, which is projected at an angle
Formula used:
Horizontal range (R) =
Where,
Complete step-by-step solution:
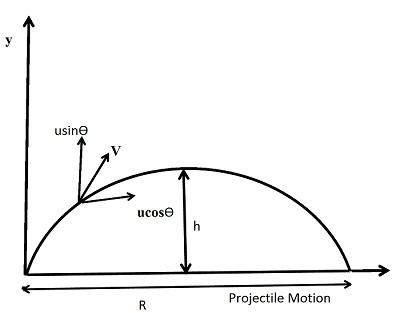
When a particle is thrown obliquely near the earth’s surface, it moves along a curved path under constant acceleration that is directed towards the centre of the earth (we assume that the particle remains close to the surface of the earth). The path of such a particle is called a projectile and the motion is called projectile motion. Air resistance to the motion of the body is to be assumed absent in projectile motion.
In a Projectile Motion, there are two simultaneous independent rectilinear motions:
Along the x-axis: uniform velocity
Along the y-axis: uniform acceleration
As, we know that horizontal range is given by the formula:
Horizontal range(R) =
The maximum value of range will depend upon
As, we know that the maximum value of
Thus, the range will be maximum when
Note: Projectile refers to an object that is in flight after being thrown or projected. The path of a projectile is ‘parabolic’. Throughout the motion, the acceleration of the projectile is constant and acts vertically downwards being equal to g. There is no acceleration acting in a horizontal direction.
Formula used:
Horizontal range (R) =
Where,
Complete step-by-step solution:

When a particle is thrown obliquely near the earth’s surface, it moves along a curved path under constant acceleration that is directed towards the centre of the earth (we assume that the particle remains close to the surface of the earth). The path of such a particle is called a projectile and the motion is called projectile motion. Air resistance to the motion of the body is to be assumed absent in projectile motion.
In a Projectile Motion, there are two simultaneous independent rectilinear motions:
Along the x-axis: uniform velocity
Along the y-axis: uniform acceleration
As, we know that horizontal range is given by the formula:
Horizontal range(R) =
The maximum value of range will depend upon
As, we know that the maximum value of
Thus, the range will be maximum when
Note: Projectile refers to an object that is in flight after being thrown or projected. The path of a projectile is ‘parabolic’. Throughout the motion, the acceleration of the projectile is constant and acts vertically downwards being equal to g. There is no acceleration acting in a horizontal direction.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




