
Maximum velocity of the particle in SHM is
A.
B.
C.
D.
Answer
481.8k+ views
Hint: In this question, it is given that the particle is performing motion in Simple harmonic motion. Simple harmonic motion of an object or particle is a forth and back movement through its equilibrium position. By using the maximum velocity given the value of average velocity can be evaluated from one extreme position to another extreme position.
Formula used:
Maximum velocity formula
Average velocity formula
Complete answer:
The position of a particle performing the simple harmonic motion can be given as a function of time
Where
Hence the velocity of the particle performing the simple harmonic motion can be obtained by differentiation of equation
Now the maximum velocity can be given by
Now as the particle is moving from one extreme point to another extreme point as from
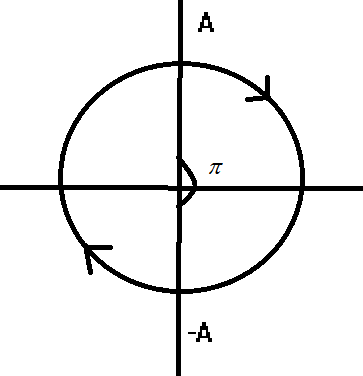
Now the total distance traveled would be given as
Now as given maximum velocity is given as
Now substituting this value of equation
Therefore the magnitude of the average velocity from one extreme point to another extreme point is given
Hence option (D) is the right answer.
Note:
Simple harmonic is considered as a very good approximation. Some conditions should be fulfilled for an oscillation that follows simple harmonic motion. The two conditions are that acceleration should be proportional to the displacement from the mean position and it should be opposite to the direction of the displacement from the mean position.
Formula used:
Maximum velocity formula
Average velocity formula
Complete answer:
The position of a particle performing the simple harmonic motion can be given as a function of time
Where
Hence the velocity of the particle performing the simple harmonic motion can be obtained by differentiation of equation
Now the maximum velocity can be given by
Now as the particle is moving from one extreme point to another extreme point as from

Now the total distance traveled would be given as
Now as given maximum velocity is given as
Now substituting this value of equation
Therefore the magnitude of the average velocity from one extreme point to another extreme point is given
Hence option (D) is the right answer.
Note:
Simple harmonic is considered as a very good approximation. Some conditions should be fulfilled for an oscillation that follows simple harmonic motion. The two conditions are that acceleration should be proportional to the displacement from the mean position and it should be opposite to the direction of the displacement from the mean position.
Recently Updated Pages
Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Trending doubts
Which one is a true fish A Jellyfish B Starfish C Dogfish class 11 biology CBSE

State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

In which part of the body the blood is purified oxygenation class 11 biology CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




