
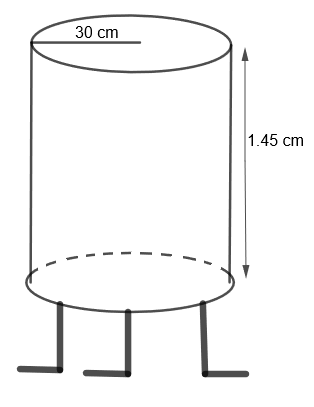
Mayank made a bird-bath for his garden in the shape of a cylinder with a hemispherical depression at one end. The height of the cylinder is 1.45m and its radius is 30 cm. Find the total surface area of the bird-bath.

Answer
511.8k+ views
Hint: First of all, draw the given bird-bath. So the total surface area of bird-bath = curved surface area of the cylinder + curved surface area of the hemisphere. Use the curved surface area of the cylinder \[=2\pi rh\] and the curved surface area of the hemisphere \[=2\pi {{r}^{2}}\] to find the total area of the bird-bath.
Complete step-by-step answer:
We are given a bird-bath in the shape of a cylinder with hemispherical depression at one end. Also, the height of the cylinder is 1.45 m and the radius is 30 cm. We have to find the total surface area of the bird-bath. Let us first see the bird-bath diagrammatically
Here, we have to find the total surface area of the bird-bath. So, we get the total surface area of the bird-bath = curved surface area of the cylinder + curved surface area of the hemisphere.
Let us consider the curved surface area of the cylinder as ‘C’ and the curved surface of the hemisphere as ‘H’. So, we get, the total surface area of the bird-bath, S = C + H …..(i)
Now, let us first find the curved surface area of the cylinder. We know that the curved surface area of the cylinder \[=2\pi rh\] where r is the radius and h is the height of the cylinder.
Also, we are given that the radius = 30 cm and height \[=1.45\times 100=145cm\]
So, by substituting the value of radius (r) and height (h), we get,
\[C=2\pi .\left( 30 \right).145c{{m}^{2}}\]
\[C=8700\pi \text{ }c{{m}^{2}}\]
Now, let us find the curved surface area of the hemisphere. We know that the curved surface area of the hemisphere, \[H=2\pi {{r}^{2}}\].
By substituting the value of r = 30 cm, we get,
\[\begin{align}
& H=2\pi .{{\left( 30 \right)}^{2}}c{{m}^{2}} \\
& H=1800\pi \text{ }c{{m}^{2}} \\
\end{align}\]
Now, by substituting the value of \[C=8700\pi \text{ }c{{m}^{2}}\] and \[H=1800\pi \text{ }c{{m}^{2}}\] in equation (i), we get,
The total surface area of the bird-bath,
\[\begin{align}
& S=\left( 8700\pi +1800\pi \right)c{{m}^{2}} \\
& S=10500\pi \text{ }c{{m}^{2}} \\
\end{align}\]
By substituting the value of \[\pi =\dfrac{22}{7}\], we get,
\[\begin{align}
& S=10500.\left( \dfrac{22}{7} \right)c{{m}^{2}} \\
& S=33000\text{ }c{{m}^{2}} \\
& \Rightarrow S=33000.\dfrac{1}{100}.\dfrac{1}{100}{{m}^{2}} \\
& S=3.3{{m}^{2}} \\
\end{align}\]
Hence, we get the total surface area of the bird-bath \[=33000c{{m}^{2}}=3.3{{m}^{2}}\]
Note: In this question, students often make this mistake of taking the values of radius and height in different units as it is given. But this is wrong. Students must convert all the parameters in 1 unit like we have taken both the radius and height in cms and then only solve the question to get the desired answer. Also, in these types of questions, always draw a proper diagram because then the question will be easier to visualize and to proceed with.
Complete step-by-step answer:
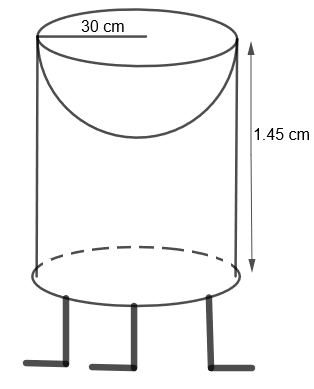
We are given a bird-bath in the shape of a cylinder with hemispherical depression at one end. Also, the height of the cylinder is 1.45 m and the radius is 30 cm. We have to find the total surface area of the bird-bath. Let us first see the bird-bath diagrammatically

Here, we have to find the total surface area of the bird-bath. So, we get the total surface area of the bird-bath = curved surface area of the cylinder + curved surface area of the hemisphere.
Let us consider the curved surface area of the cylinder as ‘C’ and the curved surface of the hemisphere as ‘H’. So, we get, the total surface area of the bird-bath, S = C + H …..(i)
Now, let us first find the curved surface area of the cylinder. We know that the curved surface area of the cylinder \[=2\pi rh\] where r is the radius and h is the height of the cylinder.
Also, we are given that the radius = 30 cm and height \[=1.45\times 100=145cm\]
So, by substituting the value of radius (r) and height (h), we get,
\[C=2\pi .\left( 30 \right).145c{{m}^{2}}\]
\[C=8700\pi \text{ }c{{m}^{2}}\]
Now, let us find the curved surface area of the hemisphere. We know that the curved surface area of the hemisphere, \[H=2\pi {{r}^{2}}\].
By substituting the value of r = 30 cm, we get,
\[\begin{align}
& H=2\pi .{{\left( 30 \right)}^{2}}c{{m}^{2}} \\
& H=1800\pi \text{ }c{{m}^{2}} \\
\end{align}\]
Now, by substituting the value of \[C=8700\pi \text{ }c{{m}^{2}}\] and \[H=1800\pi \text{ }c{{m}^{2}}\] in equation (i), we get,
The total surface area of the bird-bath,
\[\begin{align}
& S=\left( 8700\pi +1800\pi \right)c{{m}^{2}} \\
& S=10500\pi \text{ }c{{m}^{2}} \\
\end{align}\]
By substituting the value of \[\pi =\dfrac{22}{7}\], we get,
\[\begin{align}
& S=10500.\left( \dfrac{22}{7} \right)c{{m}^{2}} \\
& S=33000\text{ }c{{m}^{2}} \\
& \Rightarrow S=33000.\dfrac{1}{100}.\dfrac{1}{100}{{m}^{2}} \\
& S=3.3{{m}^{2}} \\
\end{align}\]
Hence, we get the total surface area of the bird-bath \[=33000c{{m}^{2}}=3.3{{m}^{2}}\]
Note: In this question, students often make this mistake of taking the values of radius and height in different units as it is given. But this is wrong. Students must convert all the parameters in 1 unit like we have taken both the radius and height in cms and then only solve the question to get the desired answer. Also, in these types of questions, always draw a proper diagram because then the question will be easier to visualize and to proceed with.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

The correct geometry and hybridization for XeF4 are class 11 chemistry CBSE

Water softening by Clarks process uses ACalcium bicarbonate class 11 chemistry CBSE

With reference to graphite and diamond which of the class 11 chemistry CBSE

Trending doubts
10 examples of friction in our daily life

Difference Between Prokaryotic Cells and Eukaryotic Cells

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

State and prove Bernoullis theorem class 11 physics CBSE

State the laws of reflection of light

Write down 5 differences between Ntype and Ptype s class 11 physics CBSE




