What do you mean by rectangular components of a vector? Explain how a vector can be resolved into two rectangular components in a plane.

Answer

Verified

432.2k+ views

7 likes

Hint: There are majorly two types of quantities, scalar and vector quantities. All the quantities are divided into these two categories. Scalar quantities are those quantities, which have only magnitude eg – mass, speed, pressure, etc. Vector quantities are those which have both magnitude and directions eg – weight, velocity and thrust. The special fact about vectors is that we can resolve it into components.

Complete step by step answer:
Rectangular components means the components or parts of a vector in any two mutually perpendicular axes. This could be understood by an example as illustrated below.

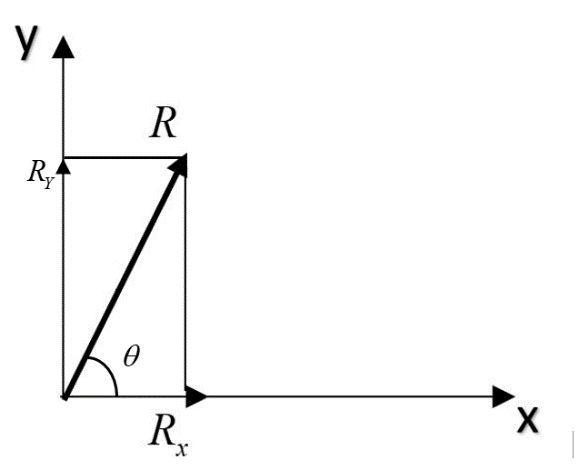
Let a vector quantity ‘R’ inclined at an angle

θ

from the x-axis. By convention, we can split the vector ‘R’ in two rectangular components. As shown in the figure, the vector ‘R’ is split into two components;

R_{x}

along x-axis and

R_{y}

along y-axis. This is an extremely important and useful property of vectors. Using it, we can solve complex problems very easily. Also, we can write the values of these components as;

R_{x} = R c o s θ

R_{y} = R s i n θ

Additional Information: For any two general vectors, we have the magnitude of their resultant

R = \sqrt{A^{2} + B^{2} + 2 A B c o s θ}

. Since we have split the given vector ‘R’ into two independent vectors, we can see that doing this won't change the magnitude of the original vector.
Here A =

R_{x} = R c o s θ

and B =

R_{y} = R s i n θ

Hence, putting in the formula:

R = \sqrt{A^{2} + B^{2} + 2 A B c o s θ}

\Rightarrow R = \sqrt{(R c o s θ)^{2} + (R s i n θ)^{2} + 2 (R c o s θ) (R s i n θ) c o s 90^{\circ}}

c o s 90^{\circ} = 0

R = \sqrt{R^{2} [(c o s θ)^{2} + (s i n θ)^{2}] + 0}

Also,

s i n^{2} θ + c o s^{2} θ = 1

So,

R = \sqrt{R^{2}} = R

Hence proved.

Note: One must not confuse that we can take the vector components only along axes that are mutually perpendicular. One can also find the component of a vector about any axis which inclination with the vector is given, provided the magnitude of the vector must not change.