Question

What do you mean by resolution of vectors? Explain how a vector can be resolved into its rectangular components in a plane?

Answer 1

Hint: Vector is a physical quantity that has both magnitude and direction and resolution that vector is known as resolution of vector. In the problem first we have to assume a vector and then divide the vector into its two components and with the help of the triangular law of addition and trigonometric formula we can calculate the required value according to the problem.

Complete step by step answer:
Resolution of vector:
It is defined as the splitting of a single vector into two or more vectors in different directions which together produce a similar effect as it produced by a single vector itself. And the vector which formed after splitting is known as the component vectors.
Two component of resolved vectors are:
Horizontal Component
Vertical Component
Horizontal component:
It is that component of the vector that moves directly in a line parallel to the horizontal axis.
Vertical Component:
It is that component of the vector that lies perpendicular to a horizontal or level plane.
Now with the help of diagram we explain the rectangular components in plane

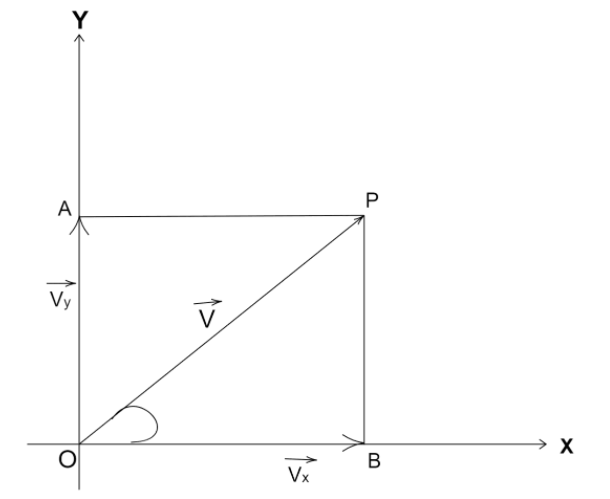
 Let us assume a vector $\overrightarrow V $ which resolves into two components $\overrightarrow {Vx} $ and $\overrightarrow {Vy} $ .
Where,
$OB = \overrightarrow {Vx} = $ Vector along the x-axis
Vector along x-axis is the horizontal component
$OA = \overrightarrow {Vy} = $ Vector along the y-axis
Vector along y-axis is the vertical component
From this we obtained our horizontal and vertical component of the vector $\overrightarrow V $ .
Now,
By drawing a line parallel to OA we will get BP which is the same as that of OA as it resolves the vector in rectangular components.
Hence,
$OA = BP = \overrightarrow {Vy} $
By applying the triangle law of addition in $\Delta OBP$ we will get,
$OP = \,OB + BP$
By putting the components we will get,
$\overrightarrow V = \overrightarrow {Vx} + \overrightarrow {Vy} \ldots \ldots \left( 1 \right)$
Here we can see the $\Delta OBP$ is a right angled triangle so we can use the trigonometric function to get the angular component along the x and y axis as well as the magnitude of the vector, respectively
In $\Delta OBP$,
Here $\theta $ is the angle between OP and OB.
$\cos \theta = \dfrac{{Base}}{{Hypotenuse}} = \dfrac{{OB}}{{OP}}$
$ \Rightarrow OP\cos \theta = OB$
Putting the component is pace of OP and OB,
$\overrightarrow V \cos \theta = \overrightarrow {Vx} \ldots \ldots \left( 2 \right)$
Similarly,
$\sin \theta = \dfrac{{Height}}{{Hypotenuse}} = \dfrac{{BP}}{{OP}}$
$ \Rightarrow OP\sin \theta = BP$
Putting the component is pace of OP and BP,
$\overrightarrow V \sin \theta = \overrightarrow {Vy} \ldots \ldots \left( 3 \right)$
Dividing equation $\left( 3 \right)$ by $\left( 2 \right)$ we will get,
$\dfrac{{\overrightarrow V \sin \theta }}{{\overrightarrow V \cos \theta }} = \dfrac{{\overrightarrow {Vy} }}{{\overrightarrow {Vx} }}$
Cancelling the common terms we will get,
$\dfrac{{\sin \theta }}{{\cos \theta }} = \dfrac{{\overrightarrow {Vy} }}{{\overrightarrow {Vx} }}$
$ \Rightarrow \tan \theta = \dfrac{{\overrightarrow {Vy} }}{{\overrightarrow {Vx} }}$
Squaring and adding equation $\left( 2 \right)$ and $\left( 3 \right)$ we will get,
${\left( {\overrightarrow V \cos \theta } \right)^2} + {\left( {\overrightarrow V \sin \theta } \right)^2} = {\left( {\overrightarrow {Vy} } \right)^2} + {\left( {\overrightarrow {Vx} } \right)^2}$
$ \Rightarrow {\left( {\overrightarrow V } \right)^2}{\cos ^2}\theta + {\left( {\overrightarrow V } \right)^2}{\sin ^2}\theta = {\left( {\overrightarrow {Vy} } \right)^2} + {\left( {\overrightarrow {Vx} } \right)^2}$
$ \Rightarrow {\left( {\overrightarrow V } \right)^2}\left( {{{\sin }^2}\theta + {{\cos }^2}\theta } \right) = {\left( {\overrightarrow {Vy} } \right)^2} + {\left( {\overrightarrow {Vx} } \right)^2}$
$ \Rightarrow {\left( {\overrightarrow V } \right)^2} = {\left( {\overrightarrow {Vy} } \right)^2} + {\left( {\overrightarrow {Vx} } \right)^2}$
We know,
${\cos ^2}\theta + {\sin ^2}\theta = 1$
Now on further solving we will egt,
$\overrightarrow V = \sqrt {{{\left( {\overrightarrow {Vy} } \right)}^2} + {{\left( {\overrightarrow {Vx} } \right)}^2}} $

Note:
A vector can be resolved in two different types: one is resolving the vector into its rectangular component and the other one is resolving the vectors in the triangular component. Remember we use this angular component magnitude to solve a problem related to resolution of vectors. Note that Resolution of rectangular components is also possible in three dimensions.