
What is meant by banking of roads? Obtain an expression for the maximum speed with which a vehicle can safely negotiate a curved road banked at an angle
Answer
451.8k+ views
2 likes
Hint: Banking of roads refers to when there is an angle between the surface of the road with the horizontal, that is, the road is inclined. This incline in the road helps in turning since the inclined direction of the normal force has a component which provides the centripetal force necessary for completing a curve.
Formula used:
For a body of mass
For a body in static equilibrium, the summation of all forces
Complete step-by-step answer:
When a car goes on a curved road, it requires a certain centripetal force to stay on the curved path and complete the turn. This centripetal force acts towards the center of the circle of the curve and constantly changes the direction of the car to help it to stay on the circular path.
Banking of roads refers to the concept that the surface of the road is inclined with the horizontal. This angle is known as the angle of inclination or the angle of banking.
When the road is banked the normal force provided by the road on the car provides a component which is in the direction of the centripetal force. Hence, when the road is banked, it is easier for a car to take the turn at a higher speed.
To obtain the expression for the maximum speed with which a vehicle can negotiate a curve on a banked road with angle
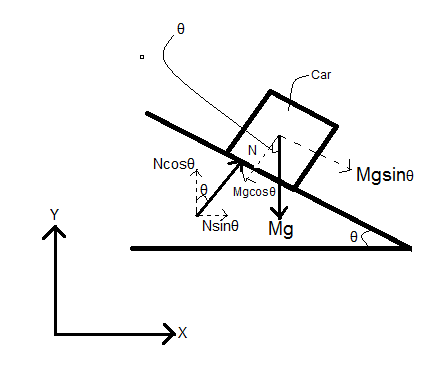
Let the mass of the car be
For a body of mass
For a body in static equilibrium, the summation of all forces
First, let us analyze the forces in the Y-direction with the forces in the positive direction of the axis being considered positive. Since, the car does not move in the y – direction, the summation of the forces must be zero.
Therefore, according to the free body diagram, using (2), we get,
Now, in the positive X – direction, the summation of forces must be equal to the centripetal force for the turn. Forces in the positive X – direction are considered positive.
Therefore, according to the free body diagram and using (1), we get,
Square rooting both sides, we get,
Therefore, the maximum speed at which the car can negotiate the turn will be
Note: It is always good to approach problems of mechanics by drawing a free body diagram and apply some rules of geometry. This helps in understanding the problem a lot and devising relations between different variables, sometimes even by geometry. Drawing a proper free body diagram is an essential skill that cannot be understated.
Students might be thinking that if
Formula used:
For a body of mass
For a body in static equilibrium, the summation of all forces
Complete step-by-step answer:
When a car goes on a curved road, it requires a certain centripetal force to stay on the curved path and complete the turn. This centripetal force acts towards the center of the circle of the curve and constantly changes the direction of the car to help it to stay on the circular path.
Banking of roads refers to the concept that the surface of the road is inclined with the horizontal. This angle is known as the angle of inclination or the angle of banking.
When the road is banked the normal force provided by the road on the car provides a component which is in the direction of the centripetal force. Hence, when the road is banked, it is easier for a car to take the turn at a higher speed.
To obtain the expression for the maximum speed with which a vehicle can negotiate a curve on a banked road with angle

Let the mass of the car be
For a body of mass
For a body in static equilibrium, the summation of all forces
First, let us analyze the forces in the Y-direction with the forces in the positive direction of the axis being considered positive. Since, the car does not move in the y – direction, the summation of the forces must be zero.
Therefore, according to the free body diagram, using (2), we get,
Now, in the positive X – direction, the summation of forces must be equal to the centripetal force for the turn. Forces in the positive X – direction are considered positive.
Therefore, according to the free body diagram and using (1), we get,
Square rooting both sides, we get,
Therefore, the maximum speed at which the car can negotiate the turn will be
Note: It is always good to approach problems of mechanics by drawing a free body diagram and apply some rules of geometry. This helps in understanding the problem a lot and devising relations between different variables, sometimes even by geometry. Drawing a proper free body diagram is an essential skill that cannot be understated.
Students might be thinking that if
Latest Vedantu courses for you
Grade 10 | CBSE | SCHOOL | English
Vedantu 10 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹34,850 per year
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
Which one is a true fish A Jellyfish B Starfish C Dogfish class 11 biology CBSE

State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

In which part of the body the blood is purified oxygenation class 11 biology CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




