Question

What is meant by the initial point of a vector?

Answer 1

Hint: To do this question, we should know from where does the vector originate. We make a vector by joining two points. From these two points one is the initial point and the other one is a terminal point.

Complete step by step solution:
In the above question, we know that

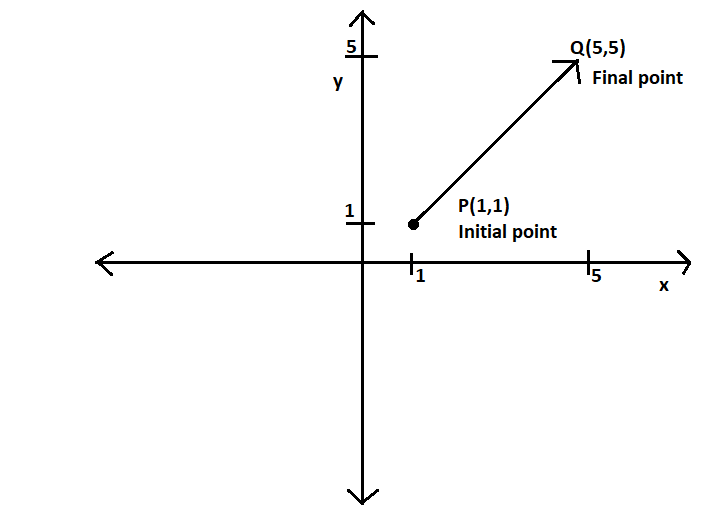
Geometrically, a vector is a length in a direction.
Also, a vector is a directed line segment. A vector (unlike a line segment) goes from one point to another.
As we know that,
A line segment has two endpoints and a length. It is a length in a particular location.
Similarly,
A vector has only a length and a direction. But we like to represent vectors using line segments.
When we try to represent a vector using a line segment, we need to distinguish one direction along the segment from the other direction. Part of doing this (or one way of doing it) is to distinguish the two endpoints by labelling one of them "initial" and the other "terminal".
 An initial point is a point from which a vector originates.
For example, using $2$ dimensional coordinates:
There is a line segment connecting the points $\left( {0,1} \right)$ and $\left( {5,1} \right)$. We can describe the same segment by saying that it connects $\left( {5,1} \right)$ and $\left( {0,1} \right)$. (It is a horizontal line segment of length $5$.)
There is also a vector from $\left( {0,1} \right)$ to $\left( {5,1} \right)$. (Some ways of describing it: the x coordinates are increasing, the vector points to the right, the initial point is $\left( {0,1} \right)$, the terminal point is $\left( {5,1} \right)$.) and a different vector from $\left( {5,1} \right)$ to $\left( {0,1} \right)$ (The x-coordinates are decreasing, the vector points to the left, the initial point is $\left( {5,1} \right)$), the terminal point is $\left( {0,1} \right)$.)
The vector from \[(4,7)\;\]to \[(9,7)\] is the same vector as from $\left( {0,1} \right)$ to $\left( {5,1} \right)$, (It has the same magnitude and the same direction.)
But it has a different initial point.

Note:
When a vector is represented as a line segment, the starting point is called the Initial Point of a Vector. The components and the magnitudes of a vector can be found out with the help of the initial point of a vector.