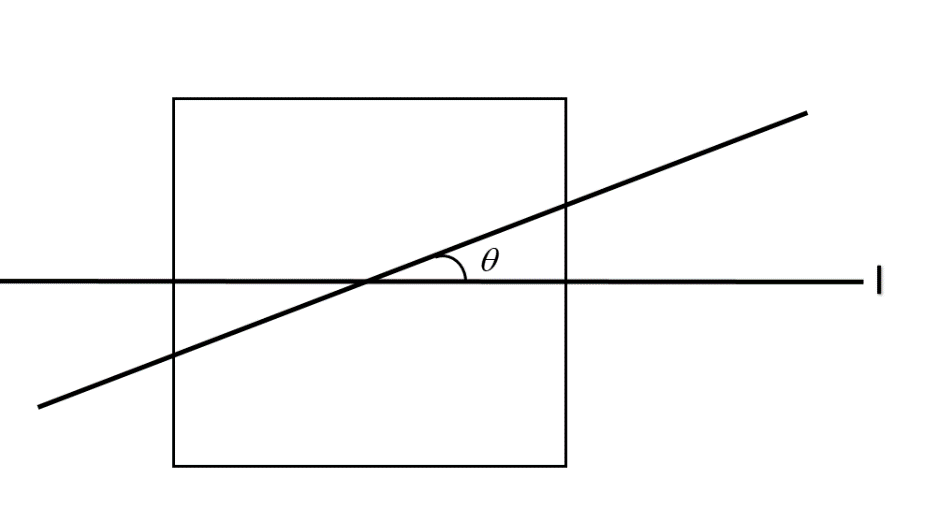
MI of a plane square lamina about an axis through its centre and parallel to one of its side is I. Then MI ‘I’ about an axis at an angle $\theta$ in the plane of the lamina passing through its centre is:

$\text{A.}\quad I$$\text{B.}\quad Cos^2 \theta$$\text{C.}\quad I sin^2\theta$$\text{D.}\quad Icos^2[\theta /2]$

Question

MI of a plane square lamina about an axis through its centre and parallel to one of its side is I. Then MI ‘I’ about an axis at an angle $θ$ in the plane of the lamina passing through its centre is:

$A. I$
$B. C o s^{2} θ$
$C. I s i n^{2} θ$
$D. I c o s^{2} [θ / 2]$

$\text{A.}\quad I$$\text{B.}\quad Cos^2 \theta$$\text{C.}\quad I sin^2\theta$$\text{D.}\quad Icos^2[\theta /2]$

Vedantu Content Team · Accepted Answer

Hint: To find the moment of inertia of any shape about an unknown axis, first we need to know the moment of inertia of the shape about an axis either perpendicular to it or parallel to it. If we know the moment of inertia of a shape about an axis passing through the centre of mass of the body, then we can find the moment of inertia about any axis parallel to it by the use of parallel axis theorem.Complete answer: Here, we are given the moment of inertia of the square about the axis ‘I’.We can use this information to compute the moment of inertia about any axis which is similar to this one. Hence the moment of inertia about an axis in the plane of square and perpendicular to the given axis will also be ‘I’. Now, the moment of inertia of about an axis perpendicular to the plane is given by a perpendicular axis theorem.Perpendicular axis theorem: Moment of inertia of a plane lamina about an axis perpendicular to the lamina is the sum of moment of inertia about two mutually perpendicular axis, lying in the lamina.So, $I_{Perp.} = I + I = 2I$But, the moment of inertia about an axis perpendicular to the plane will be the same for any two mutually perpendicular axes. Thus we have to choose one axis as given one and another perpendicular to it but in the plane, as shown.

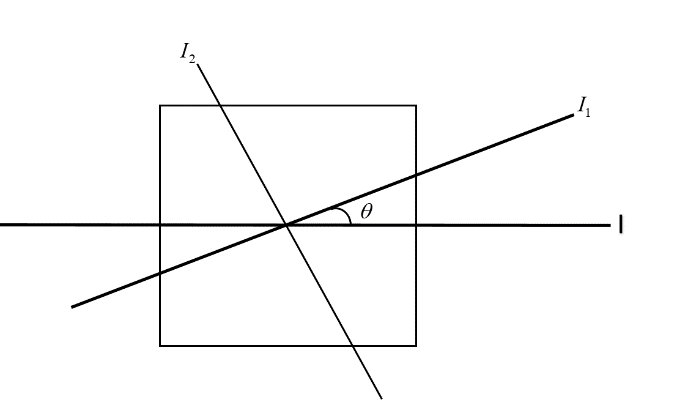
Hence $I_1 + I_2 = 2I$Now, as this case is of a square. Hence any axis passing through the centre and mutually perpendicular are alike.Thus $I_2 = I_1$Hence $I_1+I_1 = 2I$Or $I_1 = I$So, the correct answer is “Option A”.Note:One should note that we are liberal with the moment of inertias about different axes as the figure is symmetric. If the figure were not symmetrical (say rectangle), then we can’t go with this procedure and then the only tool that could be used is integration.

MI of a plane square lamina about an axis through its centre and parallel to one of its side is I. Then MI ‘I’ about an axis at an angle θ in the plane of the lamina passing through its centre is: A.IB.Cos2θC.Isin2θD.Icos2[θ/2]

Repeaters Course for NEET 2022 - 23

MI of a plane square lamina about an axis through its centre and parallel to one of its side is I. Then MI ‘I’ about an axis at an angle $θ$ in the plane of the lamina passing through its centre is:

$A. I$
$B. C o s^{2} θ$
$C. I s i n^{2} θ$
$D. I c o s^{2} [θ / 2]$