Question

What is the minimum coefficient of friction for a solid sphere to roll without slipping on an inclined plane of inclination $\theta $?
$\text{A}\text{. }\dfrac{2}{7}\tan \theta $
$\text{B}\text{. }\dfrac{1}{3}g\tan \theta $
$\text{C}\text{. }\dfrac{1}{2}\tan \theta $
$\text{D}\text{. }\dfrac{2}{5}\tan \theta $

Answer 1

Hint: Draw a free body diagram of the system. Compare and balance the forces to get the value of acceleration of the object. Find the friction of torque and put the value of moment of inertia of a solid ball to find another equation for acceleration. Compare these two equations to find the value of the coefficient of friction.

Complete step by step solution:
A solid ball of mass m is sliding in an inclined plane of inclination $\theta $.
Weight of the ball is mg.

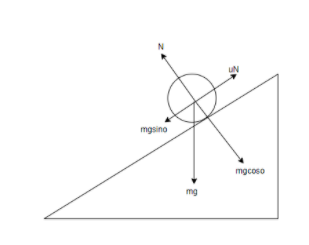
This figure is a free body diagram of the system. The solid sphere is rolling down the inclination. Here, the weight of the object is mg and N is the normal force experienced by the object. We have broken the weight of the sphere into its components $mg\cos \theta \text{ }\!\!\And\!\!\text{ }mg\sin \theta $.
Normal force N will be,
$N=mg\cos \theta $
Frictional force,
${{F}_{friction}}=\mu N=\mu mg\cos \theta $
Balancing the forces, we get,
$\begin{align}
  & ma=mg\sin \theta -\mu mg\cos \theta \\
 & a=g\sin \theta -\mu g\cos \theta \text{ }\to \text{ }1 \\
\end{align}$
The torque produced by the frictional force when two objects in contact move is called frictional torque. This torque is also a rotational force.
Friction of torque is given by,
\[\begin{align}
  & \tau =\mu N\times R \\
 & \tau =\mu mg\cos \theta \times R \\
 & I\alpha =\mu mg\cos \theta \times R\text{ }\to \text{ }2 \\
\end{align}\]
Here, $\tau $ is the frictional torque, $\mu $ is the coefficient of friction, N is the normal force on the body, g is the acceleration due to gravity, R is the radius of the solid ball, I is the moment of inertia of the ball and $\alpha $is the angular acceleration.
The moment of inertia of a solid ball can be given as,
$I=\dfrac{2}{5}m{{R}^{2}}$
Again, angular acceleration can be expressed as,
$\alpha =\dfrac{a}{R}$
Putting the values of I and $\alpha $in equation 2 gives us,
$\begin{align}
  & \dfrac{2}{5}m{{R}^{2}}\times \dfrac{a}{R}=\mu mgR\cos \theta \\
 & \dfrac{2}{5}a=\mu g\cos \theta \\
 & a=\dfrac{5}{2}\mu g\cos \theta \text{ }\to \text{ }3 \\
\end{align}$
Comparing equation 1 and 3, we get,
\[\begin{align}
  & \dfrac{5}{2}\mu g\cos \theta =g\sin \theta -\mu g\cos \theta \\
 & \dfrac{5}{2}\mu \cos \theta =\sin \theta -\mu \cos \theta \\
 & \dfrac{5}{2}\mu \cos \theta +\mu \cos \theta =\sin \theta \\
 & \dfrac{7}{2}\mu \cos \theta =\sin \theta \\
 & \mu =\dfrac{2}{7}\dfrac{\sin \theta }{\cos \theta } \\
 & \mu =\dfrac{2}{7}\tan \theta \\
\end{align}\]
So, the minimum coefficient of friction for a solid ball to roll without slipping in an inclined plane is given by \[\mu =\dfrac{2}{7}\tan \theta \]
The correct option is option (A).

Note: Definitions of the terms used in the solution,
Coefficient of friction is the measure of resistive forces applied by the two surfaces on each other while over it.
Torque can be defined as the force that causes an object to rotate about an axis.
Moment of inertia of an object can be defined as the resistance of a rotating object to its angular acceleration.
While solving this type of problem always try to draw the free body diagram. It will help you to understand the problem properly and you can imagine what you should do to solve the problem.