Question

How many minimum number of coplanar vectors which represent the same physical quantity having different magnitudes can be added to give zero resultant.
A.)2
B.)3
C.)4
D.)5

Answer 1

Hint: In order to answer this question, we should be having an idea about the Triangle Law of vector addition. The Triangle Law of vector addition helps in finding the number of coplanar vectors which will be required in order to represent the same physical quantity having different magnitudes and the addition of which will result in zero.

Step by step answer:
As the magnitude of the vectors is not equal so two vectors cannot give zero resultant. According to the Triangle Law of vector addition, a minimum of three vectors are needed to get zero resultant.

The Triangle Law of vectors states that when two vectors are represented as the two sides of a triangle, then if we want to find the magnitude and direction then the third side of the triangle, should represent the magnitude and direction of the resultant vector. A figure of the same is given below:

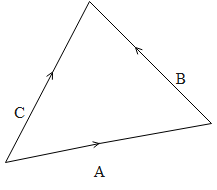
From the figure we can say that,

$\mathop {\text{C}}\limits^ \to {\text{ = }}\mathop {\text{A}}\limits^ \to {\text{ + }}\mathop {\text{B}}\limits^ \to$
Therefore, we can say that,

$\mathop {\text{A}}\limits^ \to {\text{ + }}\mathop {\text{B}}\limits^ \to - \mathop {\text{C}}\limits^ \to = 0$

So we can say that a minimum of 3 coplanar vectors is required to represent the same physical quantity having different magnitudes that can be added to give zero resultant.

Therefore, among the mentioned options, the correct answer is Option B.

Note: We can also say that if two vectors representing the sides of a triangle are in magnitude and direction which is taken in order, then the resultant sum of the vectors will be given by closing the third side of the triangle and then taking in the reverse order both in the magnitude and direction.