Question

Mirror image of a point A(1,2) about the line y=x is point B. The coordinates of a point P on the line y=x such that the triangle APB is right-angled triangle, can be
(a) (3,3)
(b) (4,4)
(c) (-1,-1)
(d) (2,2)

Answer 1

Hint: Remember that the image of the point about the line y=x can be obtained by interchanging the x-coordinate and y-coordinate of the point. For instance, the image of the point (a,b) about the line y=x is (b,a). So, we know point A and point B and as the point P lies on the line y=x, let P be (k,k). Now find the slopes of PA and PB and use the property that the product of slopes of perpendicular lines is -1 to get the value of k.

Complete step-by-step answer:
Let us start the solution to the above question by finding point B. We know that the image of the point about the line y=x can be obtained by interchanging the x-coordinate and y-coordinate of the point. For instance, the image of the point (a,b) about the line y=x is (b,a). So, the image of point A(1,2) is B(2,1).
Also, it is given that P lies on the line y=x, so, the x-coordinate and y-coordinate of P is equal and we let it be k. So, P is (k,k)
Now let us draw all the components on a graph for better visualisation.

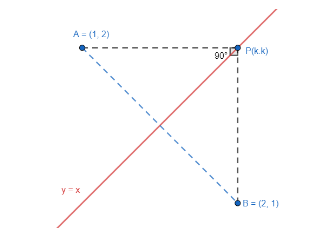
Now we know that the slope of the line passing through points $ A({{x}_{1}},{{y}_{1}})\text{ and }B({{x}_{2}},{{y}_{2}}) $ is given by $ m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}} $ . So, let us find the slope of the line PA and PB.
 $ m(PA)=\dfrac{2-k}{1-k} $
 $ m(PB)=\dfrac{1-k}{2-k} $
Now, we know that the product of slopes of perpendicular lines is -1 to get the value of k. As APB is a right-angled triangle PA must be perpendicular to PB.
 $ m(PA)m(PB)=-1 $
Now, we will put the values from the above result. On doing so, we get
 $ \dfrac{1-k}{2-k}\times \dfrac{2-k}{1-k}=-1 $
But all the terms on LHS are getting cancelled to give result 1 which makes the equation invalid, so the values of k should be such that the LHS is of the form $ \dfrac{0}{0} $ , which would eventually make the equation true. So, k can be 2 as well as 1, because for these values the numerator and denominator both are zero. Therefore, the possible values of k are 2 and 1.
Hence, P can be (1,1) and (2,2). So, the answer is option (d).

Note: Whenever you come across a situation where the equation is true for sure but terms are getting cancelled and leading to RHS and LHS not matching, always think of indeterminate form and give it a try. Also, many times it is seen that students get confused and take the difference of the x-coordinates in the numerator while finding the slope, which is completely wrong and result in the reciprocal of the slope.