Question

Moment of inertia of a thin circular plate of mass M, radius R about an axis passing through its diameter is I. The moment of inertia of a circular ring of mass M, radius R about an axis perpendicular to its plane and passing through its centre is:
1) $2I$
2) $\dfrac{I}{2}$
3) $4I$
4) $\dfrac{I}{4}$

Answer 1

Hint:Imagine a disc of radius R with a small area dm and integrate them. Here, we need to consider an imaginary ring inside the disc and then integrate it for the whole ring. The diameter is given as “I” so the radius will be half of “I”.

Complete step by step solution:

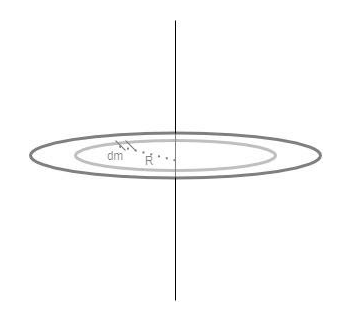
Calculate the moment of inertia of the above circular disc:

$\int {dI} = \int {dM\dfrac{R}{2}} dR$
\[ \Rightarrow \int {dI} = \dfrac{1}{2}\int {dM} RdR\]

Now, solve the integration:

\[ \Rightarrow I = \dfrac{1}{2} \times \dfrac{{{R^2}}}{2} \times M\]
\[ \Rightarrow I = \dfrac{{M{R^2}}}{4}\]

Now, the above moment of inertia is for the disc, then moment of inertia for the ring:

Here, for the ring the moment of inertia of radius R would remain constant:

$\int {dI' = \int {dM{R^2}} } $

Take the constant out:

$ \Rightarrow \int {dI' = {R^2}\int {dM} } $
\[ \Rightarrow I' = M{R^2}\]

Now, divide the moment of inertia for the disc by the ring:

\[ \Rightarrow \dfrac{I}{{I'}} = \dfrac{{\dfrac{{M{R^2}}}{4}}}{{M{R^2}}}\]
\[ \Rightarrow \dfrac{I}{{I'}} = \dfrac{{M{R^2}}}{{4 \times M{R^2}}}\]

Now, do the needed calculation:

\[ \Rightarrow \dfrac{I}{{I'}} = \dfrac{1}{4}\]
 \[ \Rightarrow 4I = I'\]

Final Answer:Option “3” is correct. Therefore, the moment of inertia of a circular ring of mass M, radius R about an axis perpendicular to its plane and passing through its centre is 4I.

Note:Here, we need to first derive the moment of inertia of the disc which is passing through the diameter and then derive the moment of inertia of the ring and after that we need to compare both the moment of inertia and find the relation between the two moment of inertia.