Question

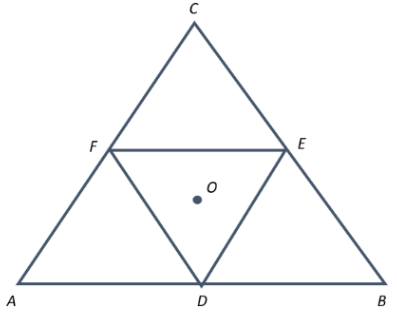
Moment of inertia of an equilateral triangular lamina ABC, about the axis passing through its centre O and perpendicular to its plane is $I_0$ as shown in the figure. A cavity DEF is cut out from the lamina, where D, E and F are the mid points of the sides. Moment of inertia of the remaining part of lamina about the same axis is:

A). $\dfrac{15}{16}I_0$
B). $\dfrac{7}{8}I_0$
C). $\dfrac{3}{4}I_0$
D). $\dfrac{31}{32}I_0$

Answer 1

Hint: Assume that mass of an equilateral triangle is concentrated about its vertices and first determine the moment of inertia of the entire lamina by finding the distance between the lamina’s centre and its vertices. Then determine the moment of inertia of the triangle DEF that is cut out, using the same assumption about mass concentrated at its own vertices and arrive at an expression for it in terms of the moment of inertia of the entire lamina. To this end, calculate the difference between the two moments of inertia thus obtained to arrive at the appropriate result for the rest of the lamina.
Formula Used:
Moment of inertia $I = \Sigma mr^2$

Complete step-by-step solution:
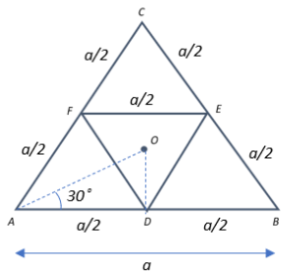
Let the length of the sides of the equilateral triangular lamina ABC be$\;a$, and let the mass of the entire lamina be$\;m$. Assuming that the mass of the lamina is concentrated about its vertices, the distance of the axis of rotation from the massive vertices can be found.
Let the distance of the axis of rotation O to one of the vertices A be OA, as shown in the figure. Since $\Delta ABC$ is equilateral, we have $\angle CAB = 60\;^{\circ}$. The line drawn from O to A bisects this angle in such a way that $\angle OAD = 30\;^{\circ}$.
From right-angled $\Delta OAD$, we have:
$cos\;30\;^{\circ} = \dfrac{AD}{OA}$
$ \Rightarrow OA = \dfrac{AD}{cos\;30\;^{\circ}} = \dfrac{\left(\dfrac{a}{2}\right)}{\left(\dfrac{\sqrt{3}}{2}\right)} = \dfrac{a}{\sqrt{3}}$
Therefore, the moment of inertia $I_0$ of the lamina acting about its centre due to all 3 of its massive vertices, with an axis perpendicular to its plane can be given as:
$I_0 = \Sigma mr^2 = 3\times m(OA)^2 = 3 \times m \times \left(\dfrac{a}{\sqrt{3}}\right)^2 = 3 \times \dfrac{ma^2}{3} = ma^2 $

Now, we are given that a cavity DEF is cut from the lamina in such a way that the points D, E and F are the midpoints of sides AB, BC and AC respectively as shown. This divides the lamina into 4 equilateral triangles such that each equilateral triangle has a mass of:
 $m^{\prime} = \dfrac{m}{4}$
We now find the moment of inertia of $\Delta DEF$ about the same axis of rotation, as we did for the entire lamina. Let the distance of the axis of rotation from one of the vertices of DEF be OD.
From $\Delta AOD$ we have:
$sin\;30\;^{\circ} = \dfrac{OD}{OA}$
$\Rightarrow OD = sin\;30\;^{\circ} \times OA = \dfrac{1}{2} \times \dfrac{a}{\sqrt{3}} = \dfrac{a}{2\sqrt{3}}$
Therefore, the moment of inertia of the equilateral triangle DEF due to all 3 of its massive vertices will be:
$I^{\prime} = 3 \times m^{\prime}(OD)^{2} = 3 \times \dfrac{m}{4} \times \left(\dfrac{a}{2\sqrt{3}}\right)^2$
$\Rightarrow I^{\prime} = 3 \times \dfrac{m}{4} \times \dfrac{a^2}{12} = 3 \times\dfrac{1}{48} \times ma^2 = \dfrac{1}{16} \times ma^2$
But we know that $I_0 = ma^2$,
Therefore, $I^{\prime} = \dfrac{1}{16} \times I_0 = \dfrac{I_0}{16}$
Once this part is removed from the lamina, the moment of inertia of the remaining part of the lamina about the same axis will be:
$I = I_0 – I^{\prime} = I_0 - \dfrac{I_0}{16} = \dfrac{16I_0 -I_0}{16} = \dfrac{15I_0}{16}$
Therefore, the correct choice would be A. $\dfrac{15}{16}I_0$

Note: It is important to understand the distinction between mass and moment of inertia. We know that in general, inertia is the object’s resistance against acceleration.
 In linear (translational) motion this is called mass [kg]. The larger the mass the tougher it is to push something to move it or slow it down.
In rotational cases, this is called the moment of inertia [kg $m^2$]. The larger the moment of inertia, the tougher it is to wing a wheel up to spin fast or slow it down. Quantitatively it is given as
$I = \Sigma mr^2$ where m is the mass of the rotating body with respect to the distance r of the mass from the axis of rotation.