Question

How is momentum conserved when the ball collides with the floor?

Answer 1

Hint: When external force on the system is zero, then according to the law of conservation of momentum, momentum is always constant. Either collision is elastic, inelastic or perfectly elastic momentum is always conserved. This conservation of momentum is independent of the size of colliding particles.

Complete answer:
According to Newton’s second law of motion, \[{{F}_{ext}}=\dfrac{dp}{dt}\].
When external forces on the system get equal to 0, i.e. \[{{F}_{ext}}=0\].

\[\Rightarrow \dfrac{dp}{dt}=0\].
\[\Rightarrow p=cons\tan t\].
Let us assume a system of two bodies of mass\[{{M}_{1}}\And {{M}_{2}}\].
Initial velocities of two bodies before collision is \[{{u}_{1}}\And {{u}_{2}}\]
Final velocities after collision is\[{{v}_{1}}\And {{v}_{2}}\].
Now linear momentum is defined as:- \[p=mv\]
Total Initial linear momentum can be expressed = \[{{M}_{1}}{{u}_{1}}+{{M}_{2}}{{u}_{2}}\]
Final linear momentum after collision can be expressed = \[{{M}_{1}}{{v}_{1}}+{{M}_{2}}{{v}_{2}}\]
Here no external force acts on this system so according to Newton’s second law , momentum remains conserved. So it can be expressed mathematically as
\[{{M}_{1}}{{u}_{1}}+{{M}_{2}}{{u}_{2}}={{M}_{1}}{{v}_{1}}+{{M}_{2}}{{v}_{2}}\]

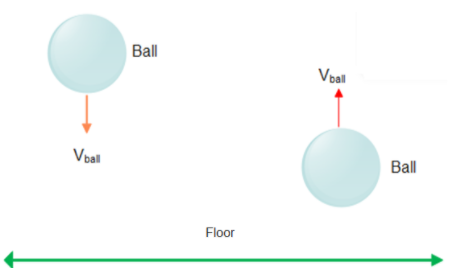
As it is given in the question that one body is a ball and other is floor. Floor can be considered as earth also.
Let us assume Mass of ball is\[{{M}_{ball}}\] and initial velocity of ball before collision is \[\overrightarrow{{{v}_{ball}}}\].
After the collision ball will bounce back let us assume it is an elastic collision so the ball will bounce back with the same velocity only direction gets reversed.
So Final velocity of ball after collision will be \[\overrightarrow{{{v}_{ball}}}\].
When the ball strikes the floor then no external force acts on this so according to Newton’s second law of motion ,momentum remains constant.
So, initially the floor is at rest so initial linear momentum is\[{{M}_{ball}}{{\overrightarrow{v}}_{ball}}\].
After collision ,the floor (earth) also attains momentum in the opposite direction of momentum of the ball to maintain the momentum of the ball.
Final linear momentum is \[{{M}_{ball}}(-\overrightarrow{{{v}_{ball}}})+{{M}_{earth}}\overrightarrow{{{v}_{earth}}}\]
As momentum is conserved so Initial linear momentum is equal to final linear momentum.
\[{{M}_{ball}}{{\overrightarrow{v}}_{ball}}={{M}_{ball}}(-\overrightarrow{{{v}_{ball}}})+{{M}_{earth}}\overrightarrow{{{v}_{earth}}}\]
\[2{{M}_{ball}}{{v}_{ball}}={{M}_{earth}}{{v}_{earth}}\]
This expression is derived when momentum remains conserved between collision of ball and floor.

Note:
If collision is not mentioned in any question then by default we should take it as elastic collision.
In elastic collision Kinetic energy is also conserved which means initial kinetic energy before collision is equal to final kinetic energy after collision while for inelastic collision kinetic energy is not conserved, initial kinetic energy is always greater than final kinetic energy.