Question

What must be the angular velocity of rotation of so that the effective acceleration due to gravity equal to zero. The Radius of the earth \[=\]\[64\times {{10}^{4}}m\]
A. \[3.3\times {{10}^{-3}}\dfrac{rad}{s}\]
B. \[3.5\times {{10}^{-3}}\dfrac{rad}{s}\]
C. \[3.7\times {{10}^{-3}}\dfrac{rad}{s}\]
D. \[3.9\times {{10}^{-3}}\dfrac{rad}{s}\]

Answer 1

Hint: Using rotation of earth and centrifugal force acting on particles we will find out the formula for acceleration due to gravity. When we assume net acceleration due to gravity is zero and angle of latitude is zero, simplifying the formula. Putting the value in the given formula we get the answer.

Complete step-by-step answer:
Acceleration due to gravity will depend on following factors:- 1. With altitude above the earth’s surface. 2. With depth below the earth’s surface. 3. Due to rotation of earth on its own axis. 4. Due to the shape of earth. As the earth rotates about its polar axis, every particle lying on its surface also revolves along a horizontal circle with the same angular velocity.

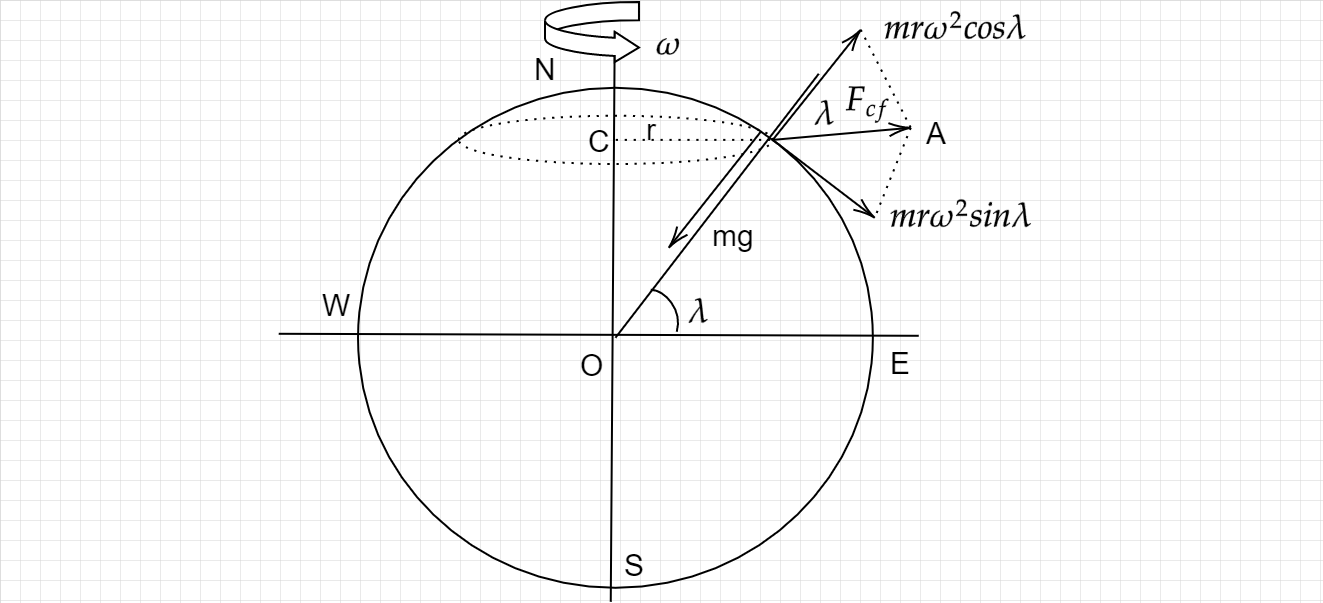
Consider a particle of mass m lying at point P, whose latitude is\[\theta \]. The particle P describes a horizontal circle of radius.
\[r=R\cos \lambda \]
The centrifugal force acting on the particle is \[{{F}_{cf}}=mr{{\omega }^{2}}\]
This force has two rectangle components: \[mr{{\omega }^{2}}\cos \lambda \]and\[mr{{\omega }^{2}}\sin \lambda \].
The component \[mr{{\omega }^{2}}\sin \lambda \]act perpendicular to mg so it cancels
 So the weight of the particle is
\[m{g}'=mg-mr{{\omega }^{2}}\cos \lambda \]
We know that from above, Acceleration due to gravity effect of rotation of the earth is given by:
\[{g}'=g-{{\omega }^{2}}R{{\cos }^{2}}\lambda \]
Where,
\[{g}'\]= effective acceleration due to gravity
\[\omega \]= angular velocity of rotation of the earth
\[\lambda \]= latitude angle
\[g\]=acceleration due to gravity
Suppose net acceleration due to gravity is zero and latitude angle is\[{{0}^{\circ }}\]. Thus,
\[{g}'=\]\[0\],\[\theta ={{0}^{\circ }}\]
Putting the above value in the formula,
\[g-{{\omega }^{2}}R\]\[=\]\[0\]
Further simplifying it,
\[g={{\omega }^{2}}R\]
\[{{\omega }^{2}}=\dfrac{g}{R}\]
We get:
\[\omega =\sqrt{\dfrac{g}{R}}\]
Now we know that (\[g\]) acceleration due to gravity is constant and the radius of the earth is given. Thus,\[g\] \[=9.8m{{s}^{-}}^{2}\]and \[R=64\times {{10}^{4}}m\]

Putting all the value in the derived formula as above
\[\omega =\sqrt{\dfrac{9.8}{64\times {{10}^{4}}}}\]

\[\omega =3.9\times {{10}^{-3}}\dfrac{rad}{s}\]

Thus, the correct option is d.

This means the value of acceleration due to gravity is highest at the point of the equator and the value of acceleration due to gravity is smallest at poles.

Note: Even for rotating the earth, the direction of rotation due to gravity it’s towards the centre of the earth both at the equator and the poles. Acceleration due to gravity increases with the increase in the latitude. If the earth stops rotating, the weight of the body would increase due to the absence of centrifugal force.