
Name the angles in the given figure.
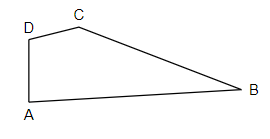

Answer
525k+ views
1 likes
Hint: We will look at the basic definition of angles and then find the angles respectively. An angle is basically the space between two intersecting lines or surfaces close to the point where they meet.
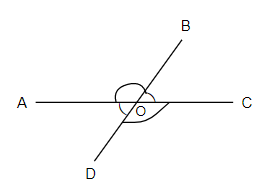
Complete step-by-step solution -
In the above figure, we have two intersecting lines
It is given in the question that we have to name the angles in the given figure.
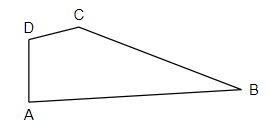
To name the angles, we have to recall the basic definition of angles and how those angles can be represented. So, angle is the space between two intersecting lines or surfaces close to the point where they meet.
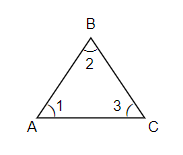
Let us consider the triangle in the figure above. In the triangle
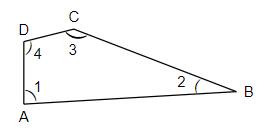
So, looking at the figure, we can make out that it is a quadrilateral with four sides,
Angle 2 can be named as
Angle 3 can be named as
Angle 4 can be named as
Hence, we have named the angles of the given figure.
Note: The students may get confused by thinking that

Complete step-by-step solution -
In the above figure, we have two intersecting lines
It is given in the question that we have to name the angles in the given figure.

To name the angles, we have to recall the basic definition of angles and how those angles can be represented. So, angle is the space between two intersecting lines or surfaces close to the point where they meet.

Let us consider the triangle in the figure above. In the triangle

So, looking at the figure, we can make out that it is a quadrilateral with four sides,
Angle 2 can be named as
Angle 3 can be named as
Angle 4 can be named as
Hence, we have named the angles of the given figure.
Note: The students may get confused by thinking that
Recently Updated Pages
Master Class 4 Maths: Engaging Questions & Answers for Success

Master Class 4 English: Engaging Questions & Answers for Success

Master Class 4 Science: Engaging Questions & Answers for Success

Class 4 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Give 10 examples for herbs , shrubs , climbers , creepers

How many millions make a billion class 6 maths CBSE

Number of Prime between 1 to 100 is class 6 maths CBSE

Four bells toll together at 900am They toll after 7811 class 6 maths CBSE

Name the countries which are larger than India class 6 social science CBSE

1 lakh Thousand class 6 maths CBSE





