
Name the type of following triangle.
Answer
528.3k+ views
1 likes
Hint: Triangles are classified in three types on the basis of length of its sides and in three types on the basis of its angles. Lengths of sides are given in question and we can calculate its angles by using sine or cosine formula.
Complete step-by-step solution -
For any
Sine formula:
Cosine formula:
Given triangle,
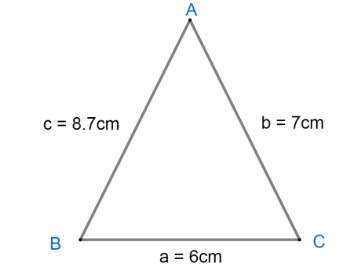
On the basis of length of sides, triangles are of three types:
1) Equilateral triangle – A triangle whose all three sides are of equal length.
2) Isosceles triangle – A triangle whose two sides are of equal length and third one is of different length.
3) Scalene triangle – A triangle whose all sides are of different length.
Since, the given triangle has all sides of different lengths, it is a scalene triangle.
On the basis of angles, triangles are of three types:
1) Acute – angled triangle – A triangle whose all angles are acute angle. (i.e.
2) Right – angle triangle – A triangle whose one angle is equal to
3) Obtuse – angled triangle – A triangle whose one angle is obtuse. (i.e.
By using cosine formula –
Similarly,
Similarly,
Graph of cos function:

From the graph, we can see that for acute angles,
Since, cos A, cos B and cos C are positive, A, B and C are acute angles.
So, the given triangle is acute – angles triangle.
Hence, the given triangle is an acute and scalene triangle.
Note: The possibility for the mistake that you put the length of sides wrong in the formula. Be careful that
a = BC
b = AC
c = AB
Complete step-by-step solution -
For any
Sine formula:

Cosine formula:
Given triangle,

On the basis of length of sides, triangles are of three types:
1) Equilateral triangle – A triangle whose all three sides are of equal length.
2) Isosceles triangle – A triangle whose two sides are of equal length and third one is of different length.
3) Scalene triangle – A triangle whose all sides are of different length.
Since, the given triangle has all sides of different lengths, it is a scalene triangle.
On the basis of angles, triangles are of three types:
1) Acute – angled triangle – A triangle whose all angles are acute angle. (i.e.
2) Right – angle triangle – A triangle whose one angle is equal to
3) Obtuse – angled triangle – A triangle whose one angle is obtuse. (i.e.
By using cosine formula –
Similarly,
Similarly,
Graph of cos function:

From the graph, we can see that for acute angles,
Since, cos A, cos B and cos C are positive, A, B and C are acute angles.
So, the given triangle is acute – angles triangle.
Hence, the given triangle is an acute and scalene triangle.
Note: The possibility for the mistake that you put the length of sides wrong in the formula. Be careful that
a = BC
b = AC
c = AB

Latest Vedantu courses for you
Grade 10 | CBSE | SCHOOL | English
Vedantu 10 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹37,300 per year
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Questions & Answers - Ask your doubts

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Science: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What is the full form of POSCO class 10 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE

How do you prove that the diagonals of a rectangle class 10 maths CBSE




