Question

Newton’s inverse square law is deduced from Kepler’s ……..of planetary motion.

Answer 1

Hint: Newton’s inverse square law is basically the law of gravitation. In total there are three Kepler’s laws of planetary motion. Hence we will see which Kepler’s law can be used to derive the Newton’s law of gravitation given by $F=G\dfrac{Mm}{{{r}^{2}}}N$ where G is the gravitational constant, M consider to be the mass of the sun, m be the mass of any planet revolving around the sun and r is the distance between them. We can begin with the expression for centripetal force acting on the planets to derive the inverse square law.

Complete answer:
To begin with let us first define all the three Kepler’s laws in brief.

The first law is called the law of orbits which explains that the planets revolve around the sun in an elliptical orbit with the sun located at its one foci. Given below is a diagram depicting the following law i.e. how the earth revolves around the sun which is at the focus S of the ellipse.

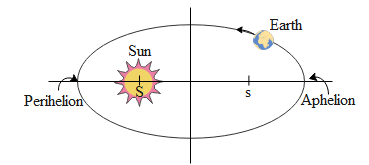
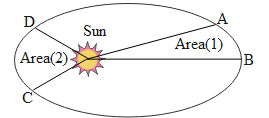
The second law also called as the law of areas states the radius vector drawn from the sun to the planet sweeps equal areas in equal interval of time i.e. the area covered by the planet in a given unit time along the elliptical path from the sun is constant. Given below is the diagram depicting this law where Area(1)=Area(2) such that the time taken by the planet to move from A to B and D to C is constant.

Kepler's third law also called the law of periods states that the square of the period of revolution of the planet around the sun is directly proportional to the cube of the distance between them. Mathematically represented as,
$\begin{align}
  & {{T}^{2}}\propto {{r}^{3}}\text{ hence we can write,} \\
 & {{T}^{2}}=k{{r}^{3}}\text{ } \\
\end{align}$
Where T is the period of revolution of the planet around the sun, r is the distance between them and k is the constant of proportionality.

Now let us consider a planet of mass m moves around the sun in a circular orbit of radius r. Let M be the mass of the sun. If v is the orbital velocity of the planet, then the required centripetal force is given by,
$F=\dfrac{m{{v}^{2}}}{r}$. But the orbital velocity is defined as $v=\dfrac{\text{Circumference}}{\text{Period of revolution}}=\dfrac{2\pi r}{T}$ where r is the radius of the orbit and T is the period of revolution. Hence substituting this in the equation of centripetal force we get,
$F=\dfrac{m{{v}^{2}}}{r}=\dfrac{m}{r}\times {{\left( \dfrac{2\pi r}{T} \right)}^{2}}=\dfrac{4{{\pi }^{2}}mr}{{{T}^{2}}}$ . But according to the law of periods ${{T}^{2}}=k{{r}^{3}}\text{ }$substituting in the adjacent equation we get,
$F=\dfrac{4{{\pi }^{2}}mr}{k{{r}^{3}}}=\dfrac{4{{\pi }^{2}}m}{k{{r}^{2}}}$ As the force between the sun and the planet is mutual it should be proportional to the mass of the sun M. Hence the factor, $\dfrac{4{{\pi }^{2}}}{k}\propto \text{M or }\dfrac{4{{\pi }^{2}}}{k}=G\text{M}$, where G is another constant. The above equation of force now becomes, $F=\dfrac{4{{\pi }^{2}}m}{k{{r}^{2}}}=\dfrac{GMm}{{{r}^{2}}}N$.This result obtained is the universal law of gravitation. We use the law of periods to derive this Newton’s inverse square law.
Hence the correct answer to the above question is Kepler’s third law.

Note:
The above inverse square law is applicable to all the two bodies in the universe. The planets orbit the sun with a particular velocity providing them a radially outward force. This is the reason why planets don’t collide with the sun and move in a particular radius.