Question

How many nodes are present in 3p orbitals? Represent diagrammatically.

Answer 1

Hint: Node is the region where the probability of finding the electrons is zero and it depends on both the principal(n) and azimuthal(l) quantum number and is calculated by the formula n-1.


Complete solution step by step:
First, we should know what an orbital is. It is the three-dimensional space around the nucleus where the probability of finding the nucleus is maximum. It does not specify the definite path and the electron can be anywhere in the region of the orbitals.
Orbitals have different shapes’ s orbital is spherical, p- orbital is dumbbell-bell shaped etc.
Node is the region in the orbital where the probability of finding the electron is negligible or almost zero. Total no of nodes can be found by the formula n-1 where n is the principal quantum number. There are two types of nodes in an orbital. They are:
Radial nodes: - It is the spherical region of the orbital where the probability of finding the electron is zero. It depends on both the principal quantum number (i.e. it determines which energy level an electron occupies) and the azimuthal quantum number (i.e. it tells us about the subshell or sublevel which an electron occupies). The principal quantum number is represented by n and the azimuthal quantum number is represented by l. The radial nodes increase as the principal quantum increases. It is calculated by the formula as n-l-1.
Here, n is the principal quantum number and l is the azimuthal quantum number.

Angular nodes: - It is the flat region of the orbital where the probability of finding the electron is zero. It depends on the azimuthal quantum number (i.e. it tells us about the subshell or sublevel which an electron occupies). The azimuthal quantum number is represented by l. The possible values of l are: 0 for s, 1 for p, 2 ford, 3 for g and so on. The number of angular nodes=l.
Here, l is the azimuthal quantum number.
Now, we have to find the number of nodes in 3p orbital.
The total no of nodes= n-1
 Here n=3, then
 Total no of nodes = 3-1
=2

No of radial nodes =n-l-1
For p, we know that l=2, then;
No of radial nodes= 3-2-1
=0
No of angular nodes=l
=2
So, the 3p orbital consists of only angular nodes.
The diagrammatic representation of node of 3p orbital is as:

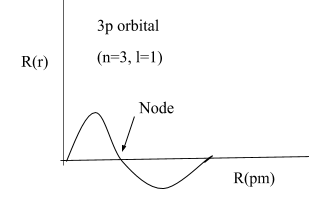
Note: Don’t get confused in the radial and angular nodes. Both are totally different but in both the probability of finding the electrons is almost zero. Radial nodes depend on both the n and l quantum numbers whereas angular nodes depend only on the l quantum number.