Question

Number of lobes present in $d_{z^2}$ orbital is:
(A) 10
(B) 5
(C) 4
(D) 2

Answer 1

Hint: To know the information about atomic orbital by referring to the quantum numbers are principal quantum number (n), angular quantum number (l), and magnetic quantum number (m). d- Orbital shape describes with the help of angular quantum number and magnetic quantum number which specifies the angular momentum of d-orbital.


Complete step by step solution:
The relation between the principal quantum number (n), angular quantum number (l), and magnetic quantum number (m) given as,
l= n-1, where n = 1, 2, 3 …
The values of m = -l….-3, -2, -1, 0, 1, 2, 3…+l
If n= 1, l=0, m= 0, the orbital represents s-orbital and only one sub orbital
If n = 2, l = 1, and m = -1, 0, +1, which represents p-orbital with three p- orbital are $p_{x,}{p}_y,p_z$
For d- orbital, n= 3, l = 2 and m = +2, +1, 0, 1, 2, which represents five d-orbital $d_{xy},d_{yz},d_{zx},d_{x^2-y^2},d_{z^2}$
The shape of the $d_{z^2}$-orbital has a lobe along the z-axis and a ring along the xy-plane, which looks like the donut with a lobe above and below.

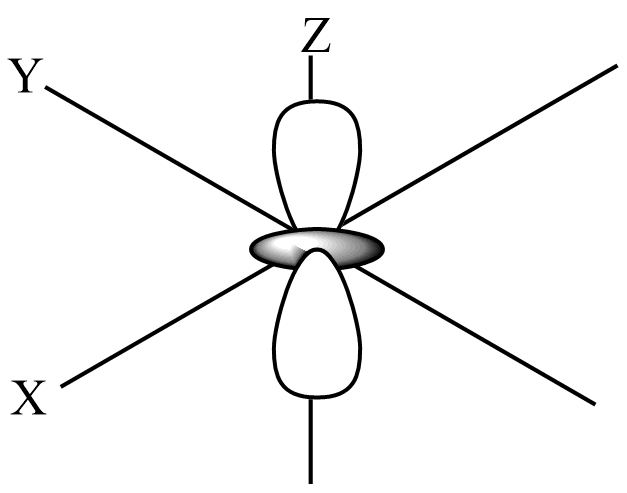
From the above shape of $d_{z^2}$-orbital, the number of lobes present in the orbital is 2. The electron density is more along the z-axis than in the $d_{z^2}$-orbital and two nodal planes are XY-plane.
Hence, the Number of lobes present in $d_{z^2}$ an orbital is 2.

The correct answer is option D.


Note: Generally, d-orbital has four lobes and 2 nodal planes. Except for $d_{z^2}$ orbital, all four orbital are four lobes between the two-axis and 2 nodal planes. For example, $d_{xy}$ orbital has 4 lobes along the XY-plane and 2 nodal planes YZ-plane, ZX-plane.