Question

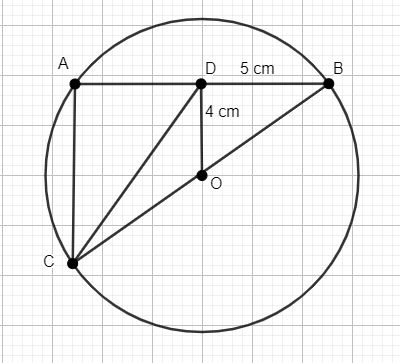
O is the centre of the circle. BC is the diameter of the circle. OD is perpendicular to AB. If OD = 4 cm and BD = 5 cm then find the value of CD.

Answer 1

Hint: To solve the question, we have to apply the Pythagorean theorem to calculate the unknown values of sides of given triangles. To solve further, apply the properties of an angle in semicircle and the properties of perpendicular bisectors for the given diagram to obtain the required values.

Complete step-by-step answer:
We know that by Pythagorean theorem, we get, in a right-angle triangle XYZ \[X{{Z}^{2}}=\text{ X}{{\text{Y}}^{2}}+Y{{Z}^{2}}\] where XZ is hypotenuse and XY, YZ are two adjacent sides of the given right-angle triangle.

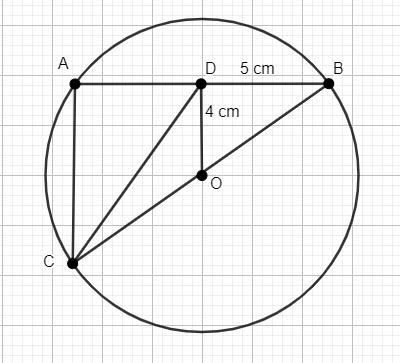
By applying the above theorem for \[\Delta ODB\], we get
\[O{{B}^{2}}=\text{ O}{{\text{D}}^{2}}+B{{D}^{2}}\]
By substituting the given value in above equation, we get
\[\begin{align}
  & O{{B}^{2}}=\text{ }{{\text{4}}^{2}}+{{5}^{2}} \\
 & O{{B}^{2}}=16+25 \\
 & O{{B}^{2}}=41 \\
 & \Rightarrow OB=\sqrt{41}cm \\
\end{align}\]
We know OC = OB since OC, OB are the radius of the given circle. Thus, we get
\[OC=\sqrt{41}cm\]
We know \[BC=OC+OB=2OB=2\sqrt{41}cm\]
Given that OB is perpendicular to AB, this implies that D is the mid-point of AB since the perpendicular drawn from the centre of a circle to its any chord always bisects the chord.
Thus, we get BD = AD = 5 cm
We know AB = AD + BD = 5 + 5 = 10 cm
We know the angle in a semicircle is always \[{{90}^{0}}\]. Thus, we get \[\angle CAB={{90}^{0}}\]
By applying the Pythagorean theorem for \[\Delta ABC\], we get
\[B{{C}^{2}}=\text{ A}{{\text{B}}^{2}}+A{{C}^{2}}\]
By substituting the given value in above equation, we get
\[\begin{align}
  & {{\left( 2\sqrt{41} \right)}^{2}}=\text{ 1}{{\text{0}}^{2}}+A{{C}^{2}} \\
 & 4\times 41=100+A{{C}^{2}} \\
 & 164=100+A{{C}^{2}} \\
 & A{{C}^{2}}=164-100 \\
 & A{{C}^{2}}=64 \\
 & AC=\sqrt{64}=\sqrt{{{8}^{2}}} \\
 & \Rightarrow AC=8cm \\
\end{align}\]
By applying the Pythagorean theorem for \[\Delta DAC\], we get
\[C{{D}^{2}}=\text{ A}{{\text{D}}^{2}}+A{{C}^{2}}\]
By substituting the given value in above equation, we get
\[\begin{align}
  & C{{D}^{2}}=\text{ }{{\text{5}}^{2}}+{{8}^{2}} \\
 & C{{D}^{2}}=\text{ }25+64 \\
 & C{{D}^{2}}=\text{ }89 \\
 & \Rightarrow CD=\sqrt{89}cm \\
\end{align}\]
Thus, the measurement of CD is equal to \[\sqrt{89}cm\]

Note: The possibility of mistake can be, not applying the Pythagorean theorem to calculate the unknown values of sides of given triangles. The other possible mistake can be, not applying the properties of an angle in semicircle and the properties of perpendicular bisectors.