Question

Observe the figure:

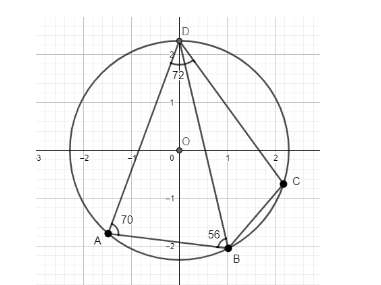
Which of the following is true?
(a) $ \angle $ BDC = 18°; $ \angle $ BCD = 110°; $ \angle $ CBD = 52°
(b) $ \angle $ BDC = 18°; $ \angle $ BCD = 110°; $ \angle $ CBD = 54°
(c) $ \angle $ BDC = 18°; $ \angle $ BCD = 120°; $ \angle $ CBD = 52°
(d) $ \angle $ BDC = 10°; $ \angle $ BCD = 110°; $ \angle $ CBD = 52°

Answer 1

Hint: We will solve this question by option verification method and use the concept that the sum of the internal angles of a triangle is 108°. We will find the angles given in the figure. With the help of the given angles, we will find one of the angles of triangle BCD. As soon as we find one angle of triangle BCD, we will see from the options which of the given options satisfy the sum of the internal angles of a triangle concept.

Complete step-by-step answer:
From the given figure, we make the following observations:
 $ \angle $ BAD = 70°……(1)
 $ \angle $ ABD = 56°……(2)
 $ \angle $ ADC = 72°……(3)
We also make note that points ABD form a triangle. Similarly, BCD also make a triangle.
Now, $ \angle $ ADC can also be written as the sum of $ \angle $ ADB and $ \angle $ BDC.
 $ \Rightarrow $ $ \angle $ ADC = $ \angle $ ADB + $ \angle $ BDC……(4)
We also know that the sum of the internal angles of a triangle is 180°.
So, in triangle ABD, $ \angle $ ABD + $ \angle $ ADB + $ \angle $ BAD = 180°
From (1) and (2), $ \angle $ BAD = 70° and $ \angle $ ABD = 56°.
 $ \Rightarrow $ 56° + $ \angle $ ADB + 70° = 180°
 $ \Rightarrow $ $ \angle $ ADB = 54°
From (4) and (3), we know that $ \angle $ ADC = $ \angle $ ADB + $ \angle $ BDC and $ \angle $ ADC = 72°
 $ \Rightarrow $ $ \angle $ ADC = $ \angle $ ADB + $ \angle $ BDC
 $ \Rightarrow $ 72° = 54° + $ \angle $ BDC
 $ \Rightarrow $ $ \angle $ BDC = 18°
Thus, we can rule out option (d).
Now, in triangle BDC, $ \angle $ BDC + $ \angle $ BCD + $ \angle $ CBD = 180°
 $ \Rightarrow $ 18° + $ \angle $ BCD + $ \angle $ CBD = 180°
 $ \Rightarrow $ $ \angle $ BCD + $ \angle $ CBD = 162°
From the options, we can see that option (a) satisfies this condition as in option (a), $ \angle $ BCD = 110°; $ \angle $ CBD = 52°, so 110° + 52° = 162°.
So, the correct answer is “Option A”.

Note: This is one method to use the concepts of sum of the internal angles of a triangle. Another principal is that the sum of the internal angles of a quadrilateral inscribed in a circle is 360°. In the figure, ABCD forms a quadrilateral. Even then, we have to use option verification as there will be two unknowns.