Question

Obtain an expression for the time of flight of a projectile.

Answer 1

Hint: Projectile motion refers to the motion of an object thrown from a horizontal surface. The object goes to a certain height and finally falls back due to gravitational force. The time of flight of a projectile is defined as the sum of time taken by the object to go up to a certain height and the time taken to fall back to the surface from where it was thrown. An expression for the time of flight of a projectile can easily be derived by separating the velocity and acceleration of the projectile, at different points of motion, into their horizontal and vertical components.

Complete step-by-step solution:
Let us consider the projectile motion of a projectile, to derive an expression for the time of flight of the projectile, as shown in the following figure.

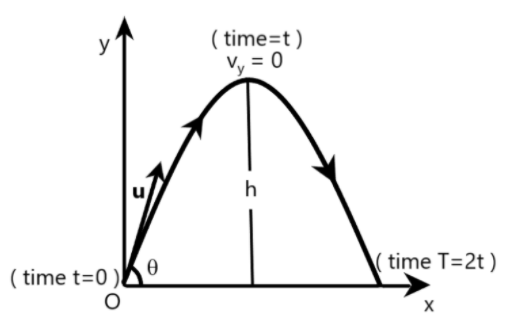
As clear from the figure, the initial position of the projectile is at $O$, when time, $t=0$. The projectile is launched from $O$ with an initial velocity of $u$, at an angle $\theta $, from the horizontal surface. Here, $\theta $ is called the angle of elevation with respect to the $x$ axis or the horizontal surface. The projectile moves with its initial velocity till a certain height $h$, away from the horizontal surface, from where it was thrown. Clearly, at a time $t$, the final velocity of the projectile $(v)$, on reaching the maximum height $(h)$ is equal to zero because the projectile stops here, before returning back to the surface.
On separating the initial velocity $(u)$ into its horizontal as well as vertical components, we have
${{u}_{x}}=u\cos \theta $
${{u}_{y}}=u\sin \theta $
where
$u$is the initial velocity of the projectile
${{u}_{x}}$ is the horizontal component of the initial velocity of the projectile
${{u}_{y}}$ is the vertical component of the initial velocity of the projectile
$\theta $ is the angle of elevation of the projectile with respect to the $x$axis
Let this set of equations be denoted by M.
In a similar manner, the acceleration of the projectile can also be separated into its horizontal as well as vertical components as given below.
${{a}_{x}}=a\cos \theta $
${{a}_{y}}=a\sin \theta $
where
$a$ is the acceleration of the projectile
${{a}_{x}}$ is the horizontal component of acceleration of the projectile
${{a}_{y}}$ is the vertical component of acceleration of the projectile
$\theta $ is the angle of elevation of the projectile with respect to the $x$axis
Let this set of equations be denoted by N.
Clearly, the set of equations denoted by N can be rewritten as
${{a}_{x}}=0$ since the projectile is moving upwards
and
${{a}_{y}}=-g=-9.8m{{s}^{-2}}$, since the acceleration of the projectile is acting against the acceleration due to gravity.
Let this set of expressions be denoted by P.
Now, let us consider the horizontal motion of the projectile from $t=0$ to time $t$ when the projectile reaches its maximum height.
Using the first equation of motion we have
${{v}_{x}}={{u}_{x}}+{{a}_{x}}t={{u}_{x}}+(0)t={{u}_{x}}$
where
${{v}_{x}}$ is the horizontal component of the final velocity of the projectile
${{u}_{x}}$ is the horizontal component of the initial velocity of the projectile
${{a}_{x}}$ is the horizontal component of acceleration of the projectile
$t$ is the time taken by projectile to reach the maximum height
Let this be equation 1.
Using the second equation of motion, we have
$x={{u}_{x}}t+\dfrac{1}{2}{{a}_{x}}{{t}^{2}}={{u}_{x}}t+\dfrac{1}{2}(0){{t}^{2}}={{u}_{x}}t$
where
$x$ is the horizontal distance covered by the projectile from $t=0$ to $t$
${{u}_{x}}$ is the horizontal component of initial velocity of the projectile
${{a}_{x}}$ is the horizontal component of acceleration of the projectile
$t$ is the time taken by projectile to reach maximum height
Let this be equation 2.
Now, let us consider the vertical motion of the projectile from $t=0$ to time $t$ when the projectile reaches a maximum height.
Using the first equation of motion we have
${{v}_{y}}={{u}_{y}}+{{a}_{y}}t={{u}_{y}}-gt=u\sin \theta -gt$
where
${{v}_{y}}$ is the vertical component of the final velocity of the projectile
${{u}_{y}}=u\sin \theta $, is the vertical component of the initial velocity of the projectile (from M)
${{a}_{y}}=-g$, is the vertical component of acceleration of the projectile (from N)
$t$ is the time taken by projectile to reach the maximum height
Let this be equation 3.
Using the second equation of motion, we have
$y={{u}_{y}}t+\dfrac{1}{2}{{a}_{y}}{{t}^{2}}={{u}_{y}}t-\dfrac{1}{2}g{{t}^{2}}=u\sin \theta t-\dfrac{1}{2}g{{t}^{2}}$
where
$y$ is the vertical distance covered by the projectile from $t=0$ to $t$
${{u}_{y}}=u\sin \theta $, is the vertical component of initial velocity of the projectile (from M)
${{a}_{y}}=-g$, is the vertical component of acceleration of the projectile (from N)
$t$ is the time taken by projectile to reach maximum height
Let this be equation 4.
Now, let us derive an expression for the time taken by the projectile to reach a maximum height of $h$.
We know that at time $t$, when the projectile is at a maximum height $h$, the vertical component of the final velocity of the projectile is equal to zero because, at this instant, the projectile comes to a stop, before falling back to the ground. Clearly, equation 3 can be written as
\[{{v}_{y}}=0\Rightarrow u\sin \theta -gt=0\Rightarrow t=\dfrac{u\sin \theta }{g}\]
where
$t$ is the time taken by the projectile to attain maximum height
$u$ is the initial velocity of the projectile
$\theta $ is the angle of elevation of the projectile
$g$ is the acceleration due to gravity
Let this be equation 5.
Now, we know that time of flight of a projectile is equal to twice the time taken by the projectile to attain its maximum height. Therefore, the time of flight of a projectile is given by
$T=2t=\dfrac{2u\sin \theta }{g}$
where
$T$ is the time of flight of a projectile
$t$ is the time taken by the projectile to attain maximum height
$u$ is the initial velocity of the projectile
$\theta $ is the angle of elevation of the projectile
$g$ is the acceleration due to gravity
Hence, the derivation.

Note: Students can also substitute the value of $t$ in equation 4 to determine the maximum height attained by the projectile before it falls down.
\[y=u\sin \theta t-\dfrac{1}{2}g{{t}^{2}}=u\sin \theta \left( \dfrac{u\sin \theta }{g} \right)-\dfrac{1}{2}g{{\left( \dfrac{u\sin \theta }{g} \right)}^{2}}=\dfrac{{{u}^{2}}{{\sin }^{2}}\theta }{2g}=h\]
where
$y=h$ is the maximum height or the vertical displacement of the projectile from $t=0$ to $t$
$u$ is the initial velocity of the projectile
$\theta $ is the angle of elevation of the projectile
$g$ is the acceleration due to gravity