
Obtain an expression of capacitance of spherical capacitor.
Answer
514.2k+ views
Hint: Here, we will proceed by assuming a spherical capacitor having some charge on the inner surface and having equal amount of charge with opposite polarity on the outer surface. Then, we will develop an equation showing the relation between the potential difference and charge.
Formulas Used- E =
Complete Step-by-Step solution:
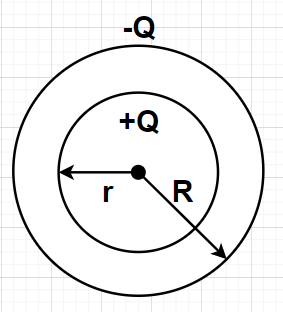
Consider a spherical capacitor having +Q charge on the inner surface and –Q on the outer surface. Let R and r be the radii of the outer surface and inner surface respectively. These two charged surfaces are separated by a radial distance of (R-r). Let the potential at the inner spherical surface be
As we know that the electric field due to a charged sphere having charge on the surface Q and radius r is given by
E =
Using above equation, electric field due to inner spherical surface having charge +Q and radius r is given by
E =
Also, we know that according to the relation between electric field and potential difference
By comparing equations (1) and (2), we can see that the LHS of both these equations are same and hence, the RHS of both these equations will be equal
Integrating on both sides of the above equation, we get
In the above equation charge (Q) is constant and hence,
where
Also, capacitance of any capacitor is given by
By substituting equation (3) in the above equation, we get
The above equation gives the expression for the capacitance of the spherical capacitor with inner surface radius as r and outer surface radius as R.
Note- It is important to note that in any capacitor, two charged surfaces (having equal and opposite charges) are separated by some distance. Capacitors are usually used to store electric charge. In this particular problem, the integration is done from the inner spherical surface to the outer spherical surface.
Formulas Used- E =
Complete Step-by-Step solution:

Consider a spherical capacitor having +Q charge on the inner surface and –Q on the outer surface. Let R and r be the radii of the outer surface and inner surface respectively. These two charged surfaces are separated by a radial distance of (R-r). Let the potential at the inner spherical surface be
As we know that the electric field due to a charged sphere having charge on the surface Q and radius r is given by
E =
Using above equation, electric field due to inner spherical surface having charge +Q and radius r is given by
E =
Also, we know that according to the relation between electric field and potential difference
By comparing equations (1) and (2), we can see that the LHS of both these equations are same and hence, the RHS of both these equations will be equal
Integrating on both sides of the above equation, we get
In the above equation charge (Q) is constant and hence,
where
Also, capacitance of any capacitor is given by
By substituting equation (3) in the above equation, we get
The above equation gives the expression for the capacitance of the spherical capacitor with inner surface radius as r and outer surface radius as R.
Note- It is important to note that in any capacitor, two charged surfaces (having equal and opposite charges) are separated by some distance. Capacitors are usually used to store electric charge. In this particular problem, the integration is done from the inner spherical surface to the outer spherical surface.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Where did Netaji set up the INA headquarters A Yangon class 10 social studies CBSE

A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Chandigarh is the capital of A Punjab B Haryana C Punjab class 10 social science CBSE




