Question

Obtain the condition for bridge balance in Wheatstone’s bridge.

Answer 1

Hint: The bridge is in the unbalanced condition where current flows through the galvanometer. Wheatstone bridge along with an operational amplifier is used to measure the physical parameters like temperature, strain, light, etc.

Complete step by step solution:

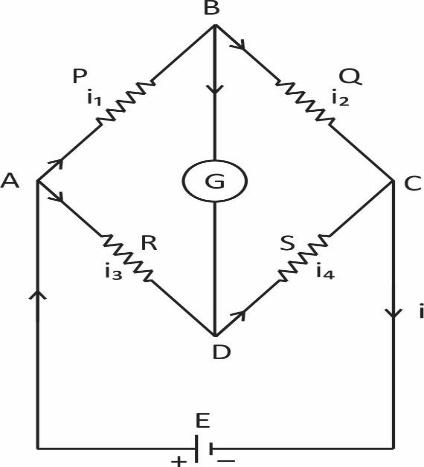
Wheatstone’s bridge is an important application of Kirchoff’s.
Wheatstone bridge consist of resistances P, Q, R and S connected to form a closed path A cell of EMF (E) is connected between point A and C. The current I from the cell is divided into \[{I_1},\,\,{I_2},\,\,{I_3}\] and \[{I_4}\] across the four branches. The current through the galvanometer is G.
Applying Kirchoff’s current law to junction B,
\[{I_1} - {I_g} - {I_3} = 0\] …. (1)
Applying Kirchoff’s current law to junction D,
\[{I_2} + {I_g} - {I_4} = 0\] … (2)
Applying Kirchoff’s voltage law to closed path ABDA
\[{I_1}P + {I_g}G - {I_2}R = 0\] … (3)
Applying Kirchoff’s voltage law to closed path ABCDA
\[{I_1}P + {I_3}Q - {I_4}S - {I_2}R = 0\] ... (4)
When the galvanometer shows zero deflection points, B and D are at same potential and \[{I_g} = 0\]. Substituting \[{I_g} = 0\] in equation (1), (2) and (3), we have
\[{I_1} = {I_3}\] …(5)
\[{I_2} = {I_4}\] …(6)
\[{I_1}P = {I_2}R\] …(7)
Substituting the values of (5) and (6) in equation (4)
\[{I_1}P + {I_1}Q - {I_2}S - {I_2}R = 0\]
\[{I_1}\left( {P + Q} \right) = {I_2}\left( {R + S} \right)\]
Dividing (8) by (7), we have
\[\dfrac{{{I_1}\left( {P + Q} \right)}}{{{I_1}\,\,P}} = \dfrac{{{I_2}\left( {R + S} \right)}}{{{I_2}R}}\]
\[\therefore \,\,\,\,\dfrac{{P + Q}}{P} = \dfrac{{R + S}}{R}\]
\[ = I + \dfrac{Q}{P} = I + \dfrac{S}{R}\]
\[\therefore \dfrac{Q}{P} = \dfrac{S}{R}\,\,\,or\,\,\,\dfrac{P}{Q} = \dfrac{R}{S}\]

Note: While solving such problems we have to keep in mind few things otherwise our answer will come wrong. We have to see how many batteries are there in the circuit. If there is only one battery in a loop then it is okay but if there are more than one we have to consider individual currents and one voltage and another will be considered and will be added or subtracted depending upon the polarities alignment of the given batteries.