Question

Obtain the relation between the magnitude of linear acceleration and angular acceleration in circular motion.

Answer 1

Hint: As a first step, you could find the relation between the linear and angular velocity. Then you could recall the definitions of linear acceleration and angular acceleration. Inter-relating the above relation you will get the required relation between linear and angular accelerations. Also, the remember radius remains constant in circular motion.

Formula used:
Linear velocity,
$v=r\omega $
Linear acceleration,
${{a}_{t}}=\dfrac{\Delta v}{\Delta t}$
Angular acceleration,
$\alpha =\dfrac{\Delta \omega }{\Delta t}$

Complete step by step solution:
In the question, we are asked to obtain the relation between the magnitudes of linear acceleration and that of angular acceleration in the case of circular motion.
For a uniform circular motion we know that the motion is in a circle with constant speed and hence constant angular velocity.

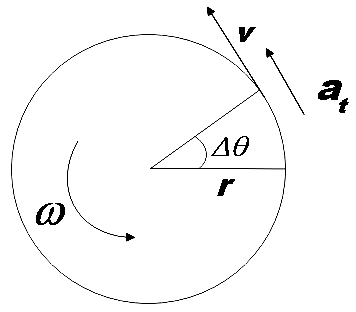
Angular velocity $\left( \omega \right)$ can be defined as the time rate of change of the angle$\theta $, that is,
$\omega =\dfrac{\Delta \theta }{\Delta t}$ ………………………………….. (1)
We also have the relation between angular velocity $\omega $ and linear velocity $v$ given by,
$v=r\omega $ …………………………………… (2)
Where r is the radius of curvature of the circle in which the motion takes place.
Angular acceleration$\left( \alpha \right)$ comes into picture when the angular velocity $\left( \omega \right)$ is not a constant. By definition, angular acceleration is the rate of change of angular velocity, that is,
$\alpha =\dfrac{\Delta \omega }{\Delta t}$ ………………………………………………… (3)
The unit of angular acceleration is$rad/{{s}^{2}}$. For increase in angular velocity, $\alpha $ is known to be positive and for decrease in$\omega $, $\alpha $ is negative.
Now let us discuss the relation of linear and angular acceleration.
The linear acceleration is found to be tangential to the circle at a particular point for circular motion and hence is called tangential acceleration ${{a}_{t}}$ and it refers to the change in the magnitude of velocity. The centripetal acceleration$\left( {{a}_{c}} \right)$ gives the changes in the direction of the velocity.
As the linear acceleration is directly proportional to time rate of velocity,
${{a}_{t}}=\dfrac{\Delta v}{\Delta t}$
From (2),
${{a}_{t}}=\dfrac{\Delta \left( r\omega \right)}{\Delta t}$
But the radius remains constant in circular motion.
${{a}_{t}}=r\dfrac{\Delta \omega }{\Delta t}$
From (3),
${{a}_{t}}=r\alpha $
Therefore, we find that linear acceleration is directly proportional to angular acceleration.

Note: From the final expression we see that, the higher the magnitude of angular acceleration is, the higher the magnitude of linear acceleration will be. Let us consider the real life example of a car. Greater angular acceleration of the car’s wheels implies greater acceleration of the car. Also, for a particular value of angular acceleration, the smaller the wheels of the car is, the smaller will be its linear acceleration.