Question

On a squared paper, sketch the following: A hexagon with exactly two lines of symmetry.

Answer 1

Hint: For drawing the required figure we need to find the number of sides and angles at each vertex. We know that a hexagon has 6 equal sides and angles. Since all the angles are equal we can find each angle using the formula \[\text{each angle = }\dfrac{{{360}^{0}}}{n}\] where \['n'\] is number of sides. As we are given two lines of symmetry one is a horizontal line and the other is a vertical line we can draw a hexagon easily with angles.

Complete step-by-step solution
Let us assume that the lines of symmetry in which one is a horizontal line of symmetry and the other is a vertical line of symmetry as

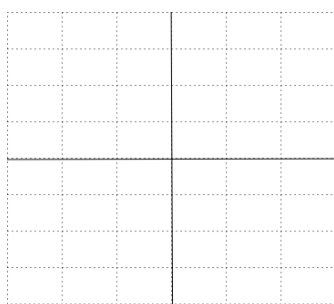
Here, we can see that the dark lines shown are the horizontal and vertical lines of symmetry.
Let us consider that the required hexagon has 2 units of length.
Now, let us plot the 2 units of length of the hexagon on the grids shown above as
 

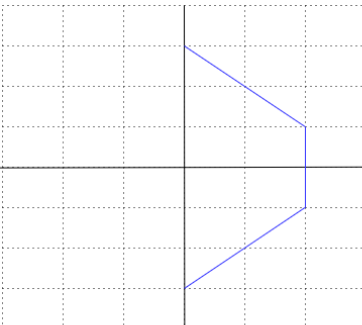
Similarly, let us draw the remaining part of the hexagon on the left side also we will get

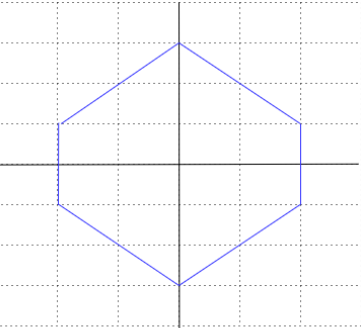
Therefore, we have drawn the required hexagon using two lines of symmetry.

Note: We can draw the hexagon without using the grids also.
Let us assume that the hexagon has some length. We know that in a hexagon all the angles are equal and have the value of \[{{60}^{0}}\]. By using some length to hexagon by keeping in mind that all the angles in a hexagon are \[{{60}^{0}}\] we can draw the hexagon as

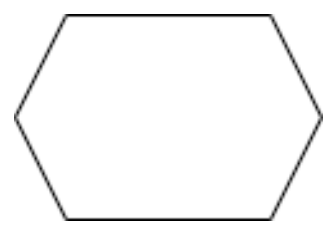
Here, there will be no need for lines of symmetry also. We just need to draw using a protractor and scale keeping all the lengths and angles as equal. Hence, we got the required hexagon.y