Question

On an open ground a motorist follows a track that turns to his left by an angle of $60^\circ $ after every 500m. Starting from a given turn, specify the displacement of the motorist at the third, sixth and eight turn. Compare the magnitude of displacement with the total path length covered by the motorist in each case.

Answer 1

Hint: Displacement as defined as the difference between the initial and the final position between the two points and distance is defined as the amount of length covered by the person in reach of a particular place. Here, imagine a motorcyclist taking $60^\circ $turn on the left after travelling a distance of 500m and draw a diagram. (It would be a hexagon)

Complete step by step solution:

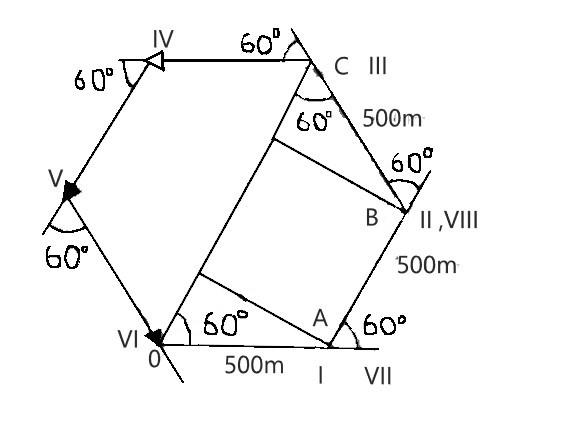
Step 1:
See the above diagram, in this diagram the magnitude of length at the 3^rd turn:

$\left| {OA + AB + BC} \right| = \left| {OC} \right|$ ;

Put the value of the length in the above relation

$ \Rightarrow 500\cos 60^\circ + 500 + 500\cos 60^\circ $ ;
$ \Rightarrow 500 \times \dfrac{1}{2} + 500 + 500 \times \dfrac{1}{2}$;

Dot the necessary calculation:

$ \Rightarrow 250 + 500 + 250$;
$ \Rightarrow \left| {OA + AB + BC} \right| = \left| {OC} \right| = 1000m$;

The above value is displacement of the motorcyclist at the 3^rd turn for the displacement:

\[{\text{Distance = }}500 + 500 + 500 = 1500m\]; (At 3^rd turn)

Now, the ratio between the displacement and distance is:

$\dfrac{{{\text{Displacement}}}}{{{\text{Distance}}}} = \dfrac{{1000}}{{1500}} = \dfrac{2}{3}$ ;

Step 2:

At 6^th turn: The initial position is same as the final position so the displacement and distance will be:

${\text{Displacement}} = 0$;
${\text{Distance}} = 6 \times 500 = 3000m$;

Now, the ratio between them is:

$\dfrac{{{\text{Displacement}}}}{{{\text{Distance}}}} = \dfrac{0}{{3000}} = 0$;


Step 3:

At the 8^th turn the displacement and the distance would be:

${\text{Displacement}} = 500\cos 60^\circ $;

Multiply and divide by “2” on the LHS:

${\text{Displacement}} = 2\left( {500} \right)\left( {\dfrac{{\cos 60^\circ }}{2}} \right)$;
$ \Rightarrow {\text{Displacement}} = \left( {1000} \right)\left( {\cos 30^\circ } \right)$;
$ \Rightarrow {\text{Displacement}} = \left( {1000} \right)\left( {\dfrac{{\sqrt 3 }}{2}} \right)$;

Do the necessary calculation:

$ \Rightarrow {\text{Displacement}} = \left( {500\sqrt 3 } \right)m$
${\text{Distance}} = 8 \times 500 = 4000m$;

The ratio between the two would be:

$\dfrac{{{\text{Displacement}}}}{{{\text{Distance}}}} = \dfrac{{500\sqrt 3 }}{{4000}} = \dfrac{{\sqrt 3 }}{8}m$;

Final Answer: The displacement at the third, sixth and eight turn of the motorcyclist is 1000m,0m and $\left( {500\sqrt 3 } \right)m$.

Note: Here, the question is not that more complex than it appears to be. We need to resolve the angle and add them together to get to the asked turn. Distance is a vector quantity so we need to resolve the angle just add the distances together.