Question

One card is drawn from a deck of $52$, what is the probability that the card drawn is an ace?

Answer 1

Hint: Here to solve this question we should have the knowledge about the configuration of a deck of $52$ cards. The deck basically consists of $4$ suits containing $13$ cards each. The $4$ suits are hearts, diamonds, spades and clubs. $13$ Cards consist of cards from A to $10$ and three picture cards queen, king, jack. A is called ace card.

Complete step-by-step answer: Probability of the event can be found out using following formula:-
Favourable number of outcomes/Total number of outcomes
Favourable outcomes mean the outcomes specifically whose probability is being asked while the total number of outcomes is the ones which cover all the possibilities.
Total number of outcomes $ = 52$ (As given in question a deck of$52$cards)
Now we will find a favourable number of outcomes for this. We have to find out the total number of ace cards in the total deck of cards.

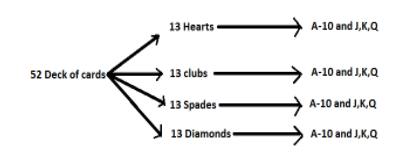
From the above flow diagram we get into the conclusion that there are $4$ ace cards in total deck of $52$cards.
Therefore the favourable outcomes are $4$
Probability that the card drawn is ace = Number of total ace cards in $52$ deck cards/Total deck of $52$ cards
$ = \dfrac{4}{{52}}$
(Cancelling numerator and denominator)
$ = \dfrac{1}{{13}}$
Hence this is the final answer.

Note: Maximum probability of an event that can come is one, so students should be careful while calculating and rechecking that answer is greater than one or not if yes then there will be a mistake. Also complete configuration of deck of cards must be remembered by heart so that one can easily find out any probability. Above flow chart mentioned in the solution will be sufficient to do the direct probability questions of this type.