Question

What is one exterior angle of a regular 16 – gon measures?

Answer 1

Hint: For solving this question you should know about the exterior angles of a polygon. We know that a circle has a total angle of \[{{360}^{\circ }}\] and we can make that as a hexadecagon of 16 – gon. For this we have to divide all the circles in four quadrants and four quadrants in four parts again. And the exterior angle will be the angle between two continuous parts in a quadrant.

Complete step by step solution:
According to the question we have to calculate the exterior angle of a hexadecagon.
Now, we see the diagram of a Hexadecagon, and what is an exterior angle.

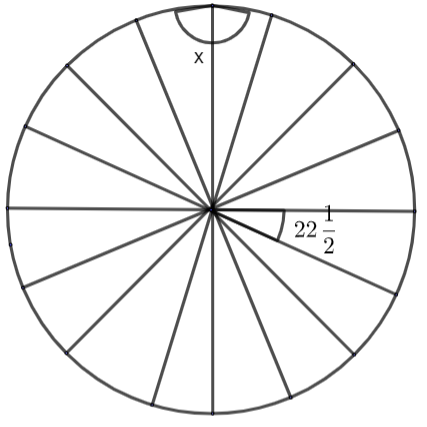
If we see the diagram then it is clear that the hexadecagon is a shape with 16 arms or sides which will make a design like a circle and the angle between two continuous sides are known as the exterior angle of that. The interior angle between two continuous sides are \[22{{\dfrac{1}{2}}^{\circ }}\].
For calculating the exterior angle of the hexadecagon we will calculate the interior angle for this.
By the diagram we can see the total value of a circle is \[{{360}^{\circ }}\].
Now, if we divide it in four quadrant then every quadrant is of \[\dfrac{{{360}^{\circ }}}{4}={{90}^{\circ }}\].
Now, we know that the formula for calculation of exterior angle is: 1 exterior angle \[=\dfrac{360}{n}\], here n is the number of sides.
For hexadecagon (16 – gon) 1 exterior angle \[=\dfrac{360}{16}={{22.5}^{\circ }}\]
If you wanted the size of 1 interior angle, subtract this from \[{{180}^{\circ }}\].
Thus: 1 interior angle \[=180-22.5={{157.5}^{\circ }}\]
So, if we calculate the exterior angle of a Hexadecagon
Then: Number of angles \[=\dfrac{360}{angle}\]
So, in a hexadecagon the number of angles is 16.
So, the angle \[=\dfrac{360}{16}={{22.5}^{\circ }}\]

Note: For calculating the exterior angle of any polygon you should use the formula or we can also calculate this by general dividation but it will be an inaccurate method for this. So, you have to use the formula. And the formula is the number of angles is the ratio of 360 and the angle.