Question

one of the parallel sides of a trapezium is 32 cm, the distance between the parallel sides is 24 cm and its area is 720 cm2. Find the length of the other parallel side.

Answer 1

Hint: In this problem, we will find the length of the other parallel side of the trapezium when one of the parallel sides is given. We will find the length of another parallel side by using the area of trapezium.
The figure of a trapezium is given below:

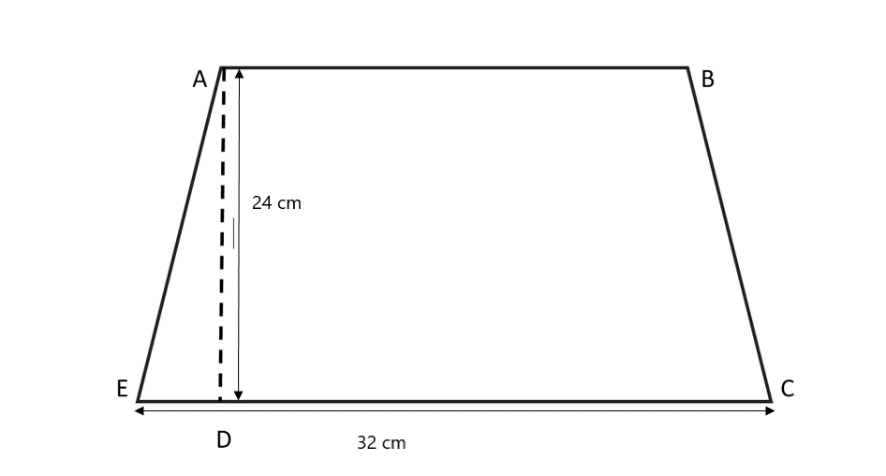
Complete step by step answer:
Where AB and EC are two parallel sides. AD is the distance between them.

Area of trapezium = $\dfrac{\left( l\left( \text{AB} \right)\text{+}l\left( \text{EC} \right) \right)}{2}l\left( \text{AD} \right)$
Where, l(AB), l(EC) and l(AD) length of side AB, EC and AD, respectively.



Given that one of the parallel sides has length 32 cm say that side be EC and the distance between parallel sides be AD = 24 cm. Area of trapezium = 720 cm2.
Area of trapezium = $\dfrac{\left( l\left( \text{AB} \right)\text{+}l\left( \text{CE} \right) \right)}{2}l\left( \text{AD} \right)$
Area of trapezium = $\dfrac{\left( l\left( \text{AB} \right)\text{+32} \right)}{2}\left( 24 \right)$
$720=\dfrac{\left( l\left( \text{AB} \right)\text{+32} \right)}{2}\left( 24 \right)$
$720=\left( l\left( \text{AB} \right)\text{+32} \right)\left( 12 \right)$
By dividing both sides by 12, we get
$\dfrac{720}{12}=\left( l\left( \text{AB} \right)\text{+32} \right)$
$l\left( \text{AB} \right)\text{+32}=60$
By subtracting 32 on both sides, we get
$l\left( \text{AB} \right)=60-32$
$l\left( \text{AB} \right)=28$
Hence the length of other parallel side AB is 28 cm.
Note:
 In this problem, one should know the Area of trapezium and its has two parallel sides with different length