Question

One of the Rectangular components of a vector of magnitude 50 units is 25 units. The angle it makes with this component is
(A) \[30^\circ \]
(B) \[60^\circ \]
(C) \[45^\circ \]
(D) \[37^\circ \]

Answer 1

Hint:Vector is defined as the physical quantity which has magnitude as well as direction.So in this question we are going to resolve a vector into two components and some mathematical calculations we can arrive at the correct result.

Complete step by step answer:
Characteristics of vectors are as follows:
1) Vectors possess magnitude as well as direction.
2) They do not obey the ordinary laws of algebra.
3) Vector changes if either magnitude or direction changes.
Any vector, $\overrightarrow a ,$can be resolved into two components. ${a_x}$is component parallel to the X-axis and ${a_y}$is component parallel to the Y-axis. Angle $\theta $gives the direction of the vector with respect to the axis.

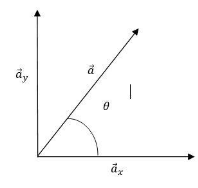
Now, according to the question.
$\therefore \left| {\overrightarrow a } \right| = 50units$
And $\left| {\overrightarrow {{a_x}} } \right|25units$
From the figure above, we observe that, \[\cos \theta = \dfrac{{\left| {\overrightarrow {{a_x}} } \right|}}{{\left| {\overrightarrow a } \right|}}\]
By substituting the given values, we get
$ \Rightarrow \cos \theta = \dfrac{{25}}{{50}}$
$ \Rightarrow \cos \theta = \dfrac{1}{2}$
\[ \Rightarrow \theta = 60^\circ \]
Therefore, the correct answer is (B) \[60^\circ \]

Note:The concept of vector is very important. In some cases, direction matters as much as the length or distance. For example, say, you are driving a car with some acceleration. Then you apply a break and the car stops. Now, the car will not go from some velocity to zero velocity in an instant. The velocity will reduce gradually and become zero. That means, there is some acceleration which is opposite to the acceleration you were applying to drive the car. Now if we do not consider the fact that both the accelerations were in opposite directions, then we will never be able to explain why the car stopped.
Some examples of vector are, displacement, velocity, acceleration, force, Weight and moment.By Parallelogram law of vectors, the magnitude of resultant vector is given by,
$R = \sqrt {{P^2} + {Q^2} + 2PQ\cos \theta } $
And the direction is given by
$\tan \alpha = \dfrac{{Q\sin \theta }}{{P + \cos \theta }}$