
How can the orbital semi-major axis, eccentricity, and period be calculated if perihelion and aphelion are known?
Answer
456.9k+ views
Hint: Ellipse is the locus of all the points in the plane. Ellipse has its centre point, major axis, minoraxis. The major axis is the axis which is the longest diameter of the ellipse. The minor axis is called the shortest diameter of the ellipse. The eccentricity defines the elongation of the ellipse. The eccentricity, e lies in between
Complete step by step answer:
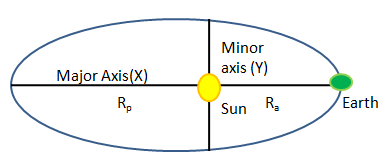
To find semi-major axis:
• We know that the longest diameter of the ellipse is called the major-axis. The half of the major axis is called the semi-major axis.
• We can find the semi-major axis by knowing the perihelion and aphelion distance.
• In the ellipse, the shortest distance from the centre of the ellipse is called perihelion. The farthest distance from the centre is called aphelion. In Greek, ‘Peri’ means close and ‘Apo’ means far. And ‘Helio’ means sun. Therefore here the ellipse is the orbit of the Earth around the sun.
• The sum of perihelion and the aphelion gives the value of the major axis as the sum defines the largest diameter. By just dividing the major axis, we can find semi-major axes.
• Lets take
Therefore,
This
To find the eccentricity:
• The value of eccentricity defines how much the ellipse is elongated. The value of eccentricity is denoted by ‘e’. The value of ‘e’ lies in between
• The perihelion value is taken as
Dividing these two values give,
Hence the value of eccentricity can be found by perihelion and aphelion.
To find period:
• According to Kepler’s 3rd law, the square of the orbital time period is directly proportional to the cube of the average distance from the sun i.e.
• We already found the value of
Note:
• Kepler’s 3rd law applies to orbiting bodies like the sun. The value of C only differs with respect to the average distance of the orbit.
• Earth’s average distance
• The Earth approaches its nearest point ‘perihelion’ with the sun in the month of January. It approaches its farthest point ‘aphelion’ in the month of July.
Complete step by step answer:

To find semi-major axis:
• We know that the longest diameter of the ellipse is called the major-axis. The half of the major axis is called the semi-major axis.
• We can find the semi-major axis by knowing the perihelion and aphelion distance.
• In the ellipse, the shortest distance from the centre of the ellipse is called perihelion. The farthest distance from the centre is called aphelion. In Greek, ‘Peri’ means close and ‘Apo’ means far. And ‘Helio’ means sun. Therefore here the ellipse is the orbit of the Earth around the sun.
• The sum of perihelion and the aphelion gives the value of the major axis as the sum defines the largest diameter. By just dividing the major axis, we can find semi-major axes.
• Lets take
Therefore,
This
To find the eccentricity:
• The value of eccentricity defines how much the ellipse is elongated. The value of eccentricity is denoted by ‘e’. The value of ‘e’ lies in between
• The perihelion value is taken as
Dividing these two values give,
Hence the value of eccentricity can be found by perihelion and aphelion.
To find period:
• According to Kepler’s 3rd law, the square of the orbital time period is directly proportional to the cube of the average distance from the sun i.e.
• We already found the value of
Note:
• Kepler’s 3rd law applies to orbiting bodies like the sun. The value of C only differs with respect to the average distance of the orbit.
• Earth’s average distance
• The Earth approaches its nearest point ‘perihelion’ with the sun in the month of January. It approaches its farthest point ‘aphelion’ in the month of July.
Recently Updated Pages
Master Class 10 Science: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Class 10 Question and Answer - Your Ultimate Solutions Guide

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Chandigarh is the capital of A Punjab B Haryana C Punjab class 10 social science CBSE

What are the public facilities provided by the government? Also explain each facility




