
Answer
488.7k+ views
Hint: In order to solve this question, we should know that a line of symmetry is a line that cuts a shape exactly into two halves. Also, we need to know that an isosceles triangle is a triangle that has only 2 sides equal to each other in length.
Complete step-by-step answer:
In this question, we have been asked to write another name of the line of symmetry of an isosceles triangle. For that let us consider an isosceles triangle ABC, such that AB = AC
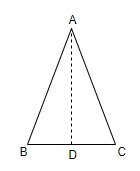
Here, we have constructed the median AD of the side BC from point A. So, we can write BD = CD. Now, we will consider triangle ABC and triangle ACD. We have been given that AB = AC and BD = CD and line AD is common. So, by SSS congruence, we can say that $\Delta ABC\cong \Delta ACD$. Hence, we can say that if we fold $\Delta ABC$ from median AD, both the parts will equally overlap each other. And we know that line of symmetry is defined as the line which cuts the shape exactly in two halves such that if we fold from the line of symmetry, both the parts will equally overlap each other.
Therefore, we can say that the line of symmetry of an isosceles triangle is the median of the third side which is not equal in length to the other two sides.
Note: We can also say that the line of symmetry of an isosceles triangle is the perpendicular bisector or altitude or median of side BC.
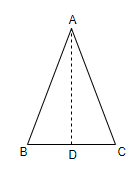
As, from the figure above, we can see that the median AD of the isosceles triangle, ABC is also an altitude and perpendicular bisector of the side BC.
Complete step-by-step answer:
In this question, we have been asked to write another name of the line of symmetry of an isosceles triangle. For that let us consider an isosceles triangle ABC, such that AB = AC

Here, we have constructed the median AD of the side BC from point A. So, we can write BD = CD. Now, we will consider triangle ABC and triangle ACD. We have been given that AB = AC and BD = CD and line AD is common. So, by SSS congruence, we can say that $\Delta ABC\cong \Delta ACD$. Hence, we can say that if we fold $\Delta ABC$ from median AD, both the parts will equally overlap each other. And we know that line of symmetry is defined as the line which cuts the shape exactly in two halves such that if we fold from the line of symmetry, both the parts will equally overlap each other.
Therefore, we can say that the line of symmetry of an isosceles triangle is the median of the third side which is not equal in length to the other two sides.
Note: We can also say that the line of symmetry of an isosceles triangle is the perpendicular bisector or altitude or median of side BC.

As, from the figure above, we can see that the median AD of the isosceles triangle, ABC is also an altitude and perpendicular bisector of the side BC.
Recently Updated Pages
How is abiogenesis theory disproved experimentally class 12 biology CBSE

What is Biological Magnification

Choose the word opposite in meaning to the given word class 8 english CBSE

Choose the word opposite in meaning to the given word class 8 english CBSE

Choose the word opposite in meaning to the given word class 8 english CBSE

Choose the word opposite in meaning to the given word class 8 english CBSE

Trending doubts
When people say No pun intended what does that mea class 8 english CBSE

Advantages and disadvantages of science

Write a letter to the Municipal Commissioner to inform class 8 english CBSE

List some examples of Rabi and Kharif crops class 8 biology CBSE

What is BLO What is the full form of BLO class 8 social science CBSE

Summary of the poem Where the Mind is Without Fear class 8 english CBSE




