Question

P is a point on either of the two lines $y+\sqrt 3 x=2$ and $y-\sqrt 3 x=2$at a distance at 5 units from their point intersection. The coordinates of the foot of the perpendicular from P on the bisector of the angle between them are
A. \[\left( {1,\dfrac{{4 + 5\sqrt 3 }}{2}} \right)\,{\rm{or}}\left( { - 1,\dfrac{{4 - 5\sqrt 3 }}{2}} \right)\]
B. \[\left( {0,\dfrac{{4 + 5\sqrt 3 }}{2}} \right)\]
C. \[\left( {0,\dfrac{{4 - 5\sqrt 3 }}{2}} \right)\]
D. \[\left( {\dfrac{5}{2},\dfrac{{5\sqrt 3 }}{2}} \right)\,\]

Answer 1

Hint: In the given solution, it is given that the point on the two sides, we have to take the negative side (2nd quadrant) and positive side (1st quadrant) lines, then we have to combine them to get the value of y.
The following is the schematic diagram to determine The coordinates of the foot.

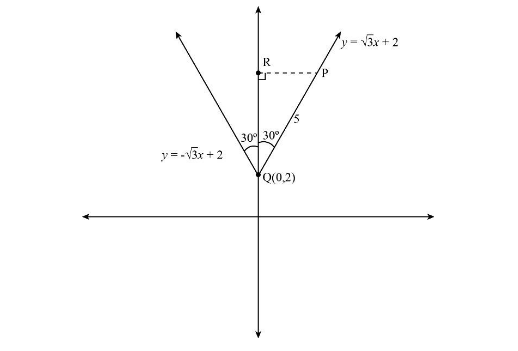
Complete step-by-step answer:
Given:
The point on the line is P.
The line one side is $y+\sqrt 3 x=2$ assuming as equation 1
The distance at which the point intersects the line is \[x = 5\] units.
The line on another side is $y-\sqrt 3 x=2$ assuming as equation 2
Solving equation 1 and 2, we get,
 \[
\Rightarrow y - \sqrt 3 x + y + \sqrt 3 x = 2 + 2\\
2y = 4\\
y = 2
\]
It means the value of y is 2.
The equation to find the coordinates of the point P,
 \[P = (x\sin \theta ,\,y + x\cos \theta )\]
Here, \[\theta \] is the angle that the line is formed by touching the y-axis. It can be taken as \[30^\circ \]
Substituting the values in the above equation, then we will get
 \[
\Rightarrow P = \pm (x\sin \theta ,\,y + x\cos \theta )\\
 = \pm \left( {5\sin 30^\circ ,\,2 + 5\cos 30^\circ } \right)\\
 = \pm \left( {\dfrac{{5\sqrt 3 }}{2},2 + \dfrac{{5\sqrt 3 }}{2}} \right)
\]
So the coordinates of the foot perpendicular to the point P on the bisector of angle can be taken as y-axis then the coordinates will be \[\left( {0,\dfrac{{4 + 5\sqrt 3 }}{2}} \right)\] .
Therefore, the coordinates of the foot of the perpendicular from P on the bisector of the angle between them are \[\left( {0,\dfrac{{4 + 5\sqrt 3 }}{2}} \right)\]
So, the correct answer is “ \[\left( {0,\dfrac{{4 + 5\sqrt 3 }}{2}} \right)\] ”.

Note: While solving the problem, we have to consider y-axis and x-axis coordinate value will become zero because the point p will lie on the y-axis line and a line should be drawn parallel to x-axis, which will be 0.