
Packing Fraction in BCC lattice is:
A.
B.
C.
D.
Answer
410.1k+ views
Hint: Packing efficiency is defined as the ratio of the volume occupied by atoms in a unit cell by the total volume of the unit cell and the efficiency of the body-centered cubic lattice is 68% and the coordination number of this BCC lattice structure is eight. Packing efficiency is also known as the atomic packing factor.
Complete answer:
It is the fraction of volume in a crystal structure that is filled up or occupied by particles constituent. Packing efficiency has no physical dimensions hence it is a dimensionless quantity.
In a Body-centered cubic unit cell, 8 atoms are present at each corner along with one center atom in the center of the cube. Each corner atom has only one-eighth of its volume within the unit cell. So BCC has a total of 2 lattice points per unit cell.
In BCC total number of atoms per unit cell is
In BCC, the center atom is touched by every corner atom. From one corner of the cube through the center and to the other corner a line is drawn and that passes through
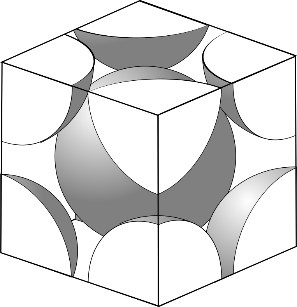
So, the length of each side of the BCC structure can be related to the radius of the atom by
We know that volume of sphere
Packing efficiency =
Substituting the values in equation (III)
Packing fraction
Packing fraction in BCC lattice
Therefore the correct answer is option (C).
Note:
The smallest part of a component in a crystal is called a unit cell. Some of the types of crystal structures are monoclinic crystal structure, triclinic crystal structure, tetragonal crystal structure, orthorhombic crystal structure, hexagonal crystal structure and rhombohedron.
Complete answer:
It is the fraction of volume in a crystal structure that is filled up or occupied by particles constituent. Packing efficiency has no physical dimensions hence it is a dimensionless quantity.
In a Body-centered cubic unit cell, 8 atoms are present at each corner along with one center atom in the center of the cube. Each corner atom has only one-eighth of its volume within the unit cell. So BCC has a total of 2 lattice points per unit cell.
In BCC total number of atoms per unit cell is
In BCC, the center atom is touched by every corner atom. From one corner of the cube through the center and to the other corner a line is drawn and that passes through

So, the length of each side of the BCC structure can be related to the radius of the atom by
We know that volume of sphere
Packing efficiency =
Substituting the values in equation (III)
Packing fraction
Packing fraction in BCC lattice
Therefore the correct answer is option (C).
Note:
The smallest part of a component in a crystal is called a unit cell. Some of the types of crystal structures are monoclinic crystal structure, triclinic crystal structure, tetragonal crystal structure, orthorhombic crystal structure, hexagonal crystal structure and rhombohedron.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




