Question

Paheli took a wire of length $10cm$. Boojho took a wire of $5cm$ of the same material and thickness. Both of them connected the wires as shown in the circuit given in figure. The current flowing in both the circuits is the same.
(1) Will the heat produced in both the cases be equal? Explain.
(2) Will the heat produced be the same if the wires taken by them are of equal lengths but different thickness? Explain.

Answer 1

Hint:Here, a circuit is given to you and different lengths of wire are connected in the circuit. The currents flowing in both the cases are the same. You are asked to comment on the heat produced in the circuits. You are also asked to comment on the heat produced if the length is the same but the thickness is different. The role of wire used here is to offer resistance to the circuit. You can consider the resistance of the wire and the formula of heat produced in order to reach your desired answer. Use Ohm’s law if required.

Complete answer:
Ohm's law is given as $j = \sigma E$, where $j$ is the current density, $E$ is the electric field and $\sigma $ is the electrical conductivity. The reciprocal of electrical conductivity is called the resistivity. Mathematically, we have, $\rho = \dfrac{1}{\sigma }$.

The current density $j$ is given as $j = \dfrac{i}{A}$, where $i$ is the current flowing inside the wire and $A$ is the area of the cross section of wire. The electric field is given as $E = \dfrac{V}{l}$, where $V$ is the applied potential difference and $l$ is the length of the wire. Let us do some substitution and rearrangements in the Ohm’s law.
$
j = \sigma E \\
\Rightarrow\dfrac{i}{A} = \left( {\dfrac{1}{\rho }} \right)\left( {\dfrac{V}{l}} \right) \\
\Rightarrow V = \left( {\rho \dfrac{l}{A}} \right)i \\
\Rightarrow V = Ri \\ $
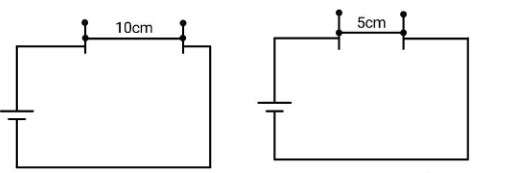
We have resistance of the wire used given as $R = \rho \dfrac{l}{A}$. The resistance depends on the material of the wire, the length of the wire and the area of the cross section of the wire.The heat produced is given as $H = \int {{i^2}Rdt} $. Since, the current in both the circuits is the same, the heats in our case can be compared on the basis of resistance of the wire used.The length of wire used by Paheli is $10cm$ and that used by Boojho is $5cm$.

So the resistance in both the cases is different and so the heat produced in the circuit will be different.If the length of wire used by Paheli and Boojho are same but the thickness of the wire is different, that is the area of cross section is different of both the wire, again the resistances of both the wires will be different and hence the heat produced will be different.

Therefore, the heat produced in both the cases will be different for (1) and the heat produced will be different if the wires taken by them are of equal lengths but different thickness for (2).

Note: We have discussed the Ohm’s law in brief. You should remember both the forms of Ohm’s law. Also keep in mind the method and approach we used to get the resistance of the wire. Remember that the resistance of a resistor depends on the material used, the length of the resistor and the area of cross section and us given by $R = \rho \dfrac{l}{A}$. Also remember the formula of heat produced in time $dt$ given as $dH = {i^2}Rdt$.