Question

What is the parametric equation of an ellipse?

Answer 1

Hint:For solving this question you should know about an ellipse and to calculate the parametric equation for it. Now we know that the equation of ellipse is $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$. Then we find the circle for it and then we draw the perpendicular to calculate the length. And then we find the value of x and y coordinates.

Complete step-by-step solution:
According to the question we have to calculate the parametric equation of an ellipse.

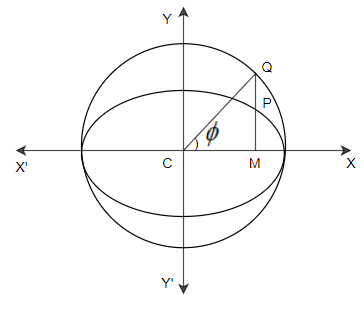
So, here we can see that a circle is on the major axis of the ellipse as diameter is called the auxiliary circle. If, $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ is an ellipse, then it’s auxiliary circle is ${{x}^{2}}+{{y}^{2}}={{a}^{2}}$. Let $P\left( x,y \right)$ be any point on the equation of the ellipse,
 $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\ldots \ldots \ldots \left( i \right)$
Now from the point P draw PM perpendicular to the major axis of the ellipse and produce MP to cut the auxiliary circle ${{x}^{2}}+{{y}^{2}}={{a}^{2}}$ at Q. Now join the point C and Q. Again let $\angle XCQ=\phi $. The angle $\angle XCQ=\phi $ is called the eccentric angle of the point P on the ellipse.
The major axis of the ellipse $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ is $AA'$ and its length is 2a. The equation of the circle is described on $AA'$ as diameter is ${{x}^{2}}+{{y}^{2}}={{a}^{2}}$. Now it is clear that CQ is in the radius of circle ${{x}^{2}}+{{y}^{2}}={{a}^{2}}$. Therefore $CM=a\cos \phi $ or $x=a\cos \phi $. Since the point $P\left( x,y \right)$ lies on the ellipse $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$. Therefore,
$\begin{align}
  & \dfrac{{{a}^{2}}{{\cos }^{2}}\phi }{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\left( \because x=a\cos \phi \right) \\
 & \Rightarrow \dfrac{{{y}^{2}}}{{{b}^{2}}}=1-{{\cos }^{2}}\phi \\
 & \Rightarrow \dfrac{{{y}^{2}}}{{{b}^{2}}}={{\sin }^{2}}\phi \Rightarrow y=b\sin \phi \\
\end{align}$
Hence the coordinates of P are $\left( a\cos \phi ,b\sin \phi \right)$. So, the parametric equation of a ellipse is $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$.

Note: During solving the parametric equation for any ellipse, we have to assure always that the ellipse’s coordinates are given and if these are to be calculated, then the parametric equation will be given with any fixed condition.