Question

Parikshit makes a cuboid of plasticine of sides 5 cm, 2 cm, 5 cm. How many such cuboids will he need to form a cube?

Answer 1

Hint- Here, we will proceed by finding the volume of one cuboid by the formula i.e., Volume of the cuboid = (Length of the cuboid)$ \times $(Breadth of the cuboid)$ \times $(Height of the cuboid) and then we will find the volume of the biggest cube using the formula i.e., Volume of the cube = ${\left( {{\text{Side of the cube}}} \right)^3}$. To find the number of cuboids required to form the biggest cube is given by dividing the volume of the biggest cube by the volume of the cuboid.

Complete step-by-step answer:

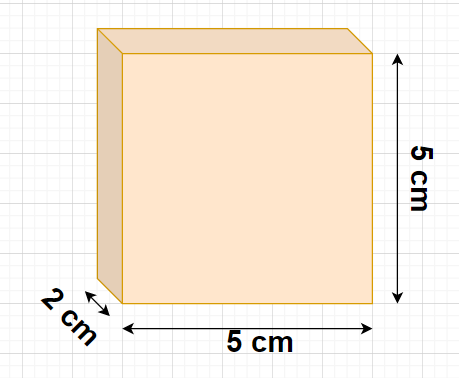
Given, Length of the cuboid of plasticine = 5 cm
Breadth of the cuboid of plasticine = 2 cm
Height of the cuboid of plasticine = 5 cm
As we know that volume of the cuboid is given by
Volume of the cuboid = (Length of the cuboid)$ \times $(Breadth of the cuboid)$ \times $(Height of the cuboid)
$ \Rightarrow $Volume of the cuboid of plasticine = 5$ \times $2$ \times $5 = 50 ${\text{c}}{{\text{m}}^3}$
Cube is a special form of cuboid in which length, breadth and height are equal i.e., all the dimensions of a cube are equal in measure.
Dimension (or side) of the biggest cube which can be formed by joining some cuboids each of sides 5 cm, 2 cm, 5 cm is equal to the LCM of the sides of the cuboid
i.e., Side of the biggest cube = LCM of 5,2,5 = 10

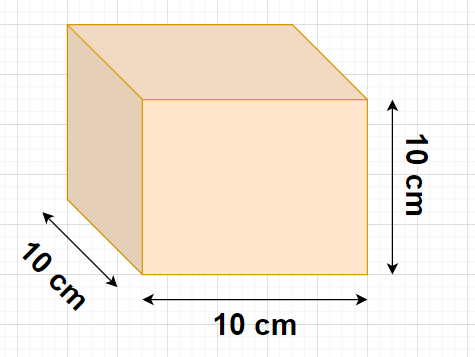
Also, we know that the volume of the cube is given by
Volume of the cube = ${\left( {{\text{Side of the cube}}} \right)^3}$
$ \Rightarrow $Volume of the biggest cube = ${\left( {{\text{10}}} \right)^3} = 1000{\text{ c}}{{\text{m}}^3}$
Since, Number of cuboids required to form the biggest cube $ = \dfrac{{{\text{Volume of the biggest cube}}}}{{{\text{Volume of the cuboid}}}} = \dfrac{{1000}}{{50}} = 20$
Therefore, 20 cuboids each of sides 5 cm, 2 cm, 5 cm will be needed to form a cube.

Note- In this particular problem, the most crucial step is that the Lowest Common Multiple (LCM) of the dimensions of the given cuboid will be equal to the side of the biggest cube. Here, the total volume of the biggest cube is formed by the elemental volumes of all the cuboids each of sides 5 cm, 2 cm, 5 cm.