Question

People of the village want to construct a road nearest to a circular village Rampur. The road cannot pass through the village. But the people want the road to be at the shortest distance from the centre of the village.
i) Which road will be the nearest to the centre of the village.
ii) If the road starts from point O which is outside the circular village and touch the boundary of the circular village at point A such that OA = 20 cm. If the straight distance of the point O from the centre of the village C is 25 cm, then find the shortest distance of the road from the centre of the village.

Answer 1

Hint: In this question, we will use the property of circle and tangent to find the nearest road and then use Pythagoras theorem to find the shortest distance to the road from the centre of the village.

Complete step by step answer:

i) According to the given question, the village Rampur is circular in shape. People of the village want to construct a road which is nearest to the circle. But this road should not pass through the village. So, the possible road will be that line to the circle which must be nearest but not cut the circle. So, this line will just touch the circle. Hence the road will be tangent to the circle which will be at the distance of radius from the centre of the circle.
ii) As given in question, C is the centre of the village. O is the starting point of the road which is constructed to the circle. Now, this road meets the village at the point A. Therefore, A is the point of contact of tangent to the circle.
Also, we are given that,
OA = 20 cm and AC = 25 cm.

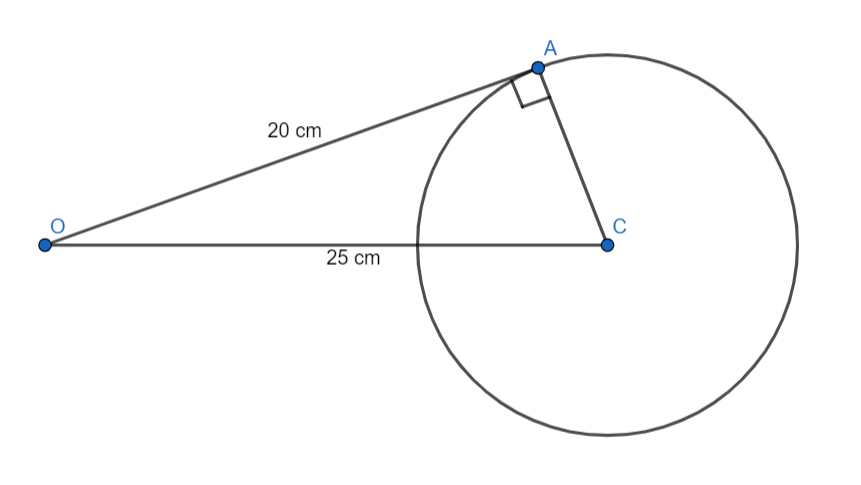
Now, we know that the tangent of the circle makes angle ${{90}^{\circ }}$ with the radius of the circle.
Therefore, triangle OAC will be a right-angle triangle, right angled at A.
So, applying Pythagoras theorem here, we get,
 $\text{A}{{\text{O}}^{\text{2}}}\text{+A}{{\text{C}}^{\text{2}}}\text{=O}{{\text{C}}^{\text{2}}}$
Putting values of AO and OC, we get,
${{\left( \text{20cm} \right)}^{\text{2}}}\text{+A}{{\text{C}}^{\text{2}}}\text{=}{{\left( \text{25cm} \right)}^{\text{2}}}$
Subtracting ${{\left( \text{20cm} \right)}^{\text{2}}}$ from both sides of the equation, we get,
$\begin{align}
  & \text{A}{{\text{C}}^{\text{2}}}\text{=}{{\left( \text{25cm} \right)}^{\text{2}}}-{{\left( \text{20cm} \right)}^{\text{2}}} \\
 & =\left( {{25}^{2}}-{{20}^{2}} \right)\text{c}{{\text{m}}^{\text{2}}} \\
\end{align}$
Writing the values of square terms, we get,
$\begin{align}
  & \text{A}{{\text{C}}^{\text{2}}}\text{=}\left( \text{625-400} \right)\text{c}{{\text{m}}^{\text{2}}} \\
 & \Rightarrow \text{A}{{\text{C}}^{2}}\text{=225c}{{\text{m}}^{\text{2}}} \\
\end{align}$
Taking square root on both sides of the equation, we get,
$\begin{align}
  & \sqrt{\text{A}{{\text{C}}^{\text{2}}}}\text{=}\sqrt{\text{225c}{{\text{m}}^{\text{2}}}} \\
 & \Rightarrow \text{AC=15cm} \\
\end{align}$
Therefore, the shortest distance to the road from the centre of the village, that is the radius of the village is 15 cm.

Note: In this type of question, when tangent from exterior point, line from centre to exterior point and radius of a circle form a triangle, where two of the lengths are known, then we always use Pythagoras theorem to find the third length.