
What is the perimeter of a quadrant of a circle with radius r=3cm?
Answer
400.5k+ views
1 likes
Hint: We are given with data that involves the radius of a circle. We are asked to find the perimeter of the quadrant that is
Complete step by step answer:
Let us first draw the diagram of the given situation.
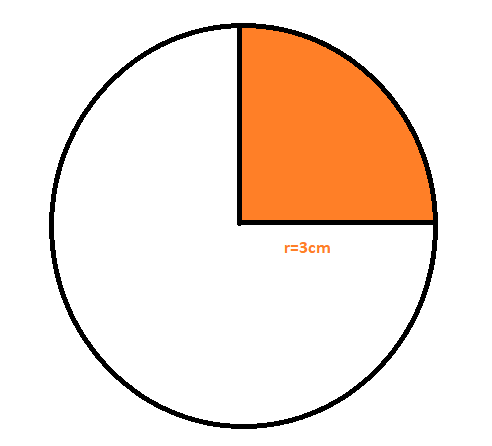
Thus the coloured portion is called the quadrant of the circle.
Now let's find the perimeter.
Putting the value of the radius we can find the perimeter.
Thus the perimeter of the quadrant is 10.71cm
Note:
Note that perimeter is the addition of the lengths of the edges or sides of the diagram. Since a circle has no edge its circumference is the only perimeter. Also note that perimeter is always measured in a single unit that is cm or m and not square quantity since it is a type of length.
Complete step by step answer:
Let us first draw the diagram of the given situation.

Thus the coloured portion is called the quadrant of the circle.
Now let's find the perimeter.
Putting the value of the radius we can find the perimeter.
Thus the perimeter of the quadrant is 10.71cm
Note:
Note that perimeter is the addition of the lengths of the edges or sides of the diagram. Since a circle has no edge its circumference is the only perimeter. Also note that perimeter is always measured in a single unit that is cm or m and not square quantity since it is a type of length.
Latest Vedantu courses for you
Grade 7 | CBSE | SCHOOL | English
Vedantu 7 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹45,300 per year
Recently Updated Pages
Master Class 10 Science: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Class 10 Question and Answer - Your Ultimate Solutions Guide

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Trending doubts
In Indian rupees 1 trillion is equal to how many c class 8 maths CBSE

List some examples of Rabi and Kharif crops class 8 biology CBSE

How many ounces are in 500 mL class 8 maths CBSE

Summary of the poem Where the Mind is Without Fear class 8 english CBSE

Advantages and disadvantages of science

How many ten lakhs are in one crore-class-8-maths-CBSE





